Question
The area of the region $$\left\{ {x,\,y\,:\,xy \leqslant 8,\,1 \leqslant y \leqslant {x^2}} \right\}$$ is-
A.
$$8\,{\log _e}2 - \frac{{14}}{3}$$
B.
$$16\,{\log _e}2 - \frac{{14}}{3}$$
C.
$$8\,{\log _e}2 - \frac{7}{3}$$
D.
$$16\,{\log _e}2 - 6$$
Answer :
$$16\,{\log _e}2 - \frac{{14}}{3}$$
Solution :
$$xy \leqslant 8,\,\,1 \leqslant y \leqslant {x^2}$$
Intersection points of $$xy= 8$$ and $$y= 1$$ is $$\left( {8,\,1} \right);xy = 8$$ and $$y = {x^2}$$ is $$\left( {2,\,4} \right)$$ and $$y = {x^2}$$ and $$y =1$$ is $$\left( {1,\,1} \right)$$
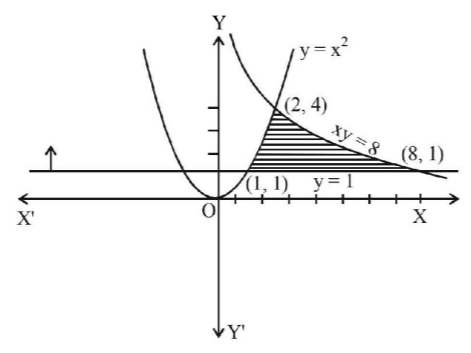
$$\eqalign{ & {\text{Required area}}\, = \int\limits_1^2 {{x^2}dx} + \int\limits_2^8 {\frac{8}{x}dx} - \int\limits_1^8 {1\,dx} \cr & = \left( {\frac{{{x^3}}}{3}} \right)_1^2 + \left( {8\ln \,x} \right)_2^8 - \left( x \right)_1^8 \cr & = \frac{8}{3} - \frac{1}{3} + 8\,\ln \,8 - 8\,\ln \,2 - \left( {8 - 1} \right) \cr & = \frac{7}{3} + 24\,\ln \,2 - 8\,\ln \,2 - 7 \cr & = 16\,\ln \,2 - \frac{{14}}{3} \cr & \therefore {\text{ Correct option is (B)}} \cr} $$
$$xy \leqslant 8,\,\,1 \leqslant y \leqslant {x^2}$$
Intersection points of $$xy= 8$$ and $$y= 1$$ is $$\left( {8,\,1} \right);xy = 8$$ and $$y = {x^2}$$ is $$\left( {2,\,4} \right)$$ and $$y = {x^2}$$ and $$y =1$$ is $$\left( {1,\,1} \right)$$

$$\eqalign{ & {\text{Required area}}\, = \int\limits_1^2 {{x^2}dx} + \int\limits_2^8 {\frac{8}{x}dx} - \int\limits_1^8 {1\,dx} \cr & = \left( {\frac{{{x^3}}}{3}} \right)_1^2 + \left( {8\ln \,x} \right)_2^8 - \left( x \right)_1^8 \cr & = \frac{8}{3} - \frac{1}{3} + 8\,\ln \,8 - 8\,\ln \,2 - \left( {8 - 1} \right) \cr & = \frac{7}{3} + 24\,\ln \,2 - 8\,\ln \,2 - 7 \cr & = 16\,\ln \,2 - \frac{{14}}{3} \cr & \therefore {\text{ Correct option is (B)}} \cr} $$