Question
The area of the region enclosed by the curves $$y = x\,{\log _e}x$$ and $$y = 2x - 2{x^2}$$ is :
A.
$$\frac{5}{{12}}$$
B.
$$\frac{7}{{12}}$$
C.
$$1$$
D.
$$\frac{4}{7}$$
Answer :
$$\frac{7}{{12}}$$
Solution :
Curve tracing, $$y = x\,{\log _e}x$$
Clearly $$x > 0,$$
For $$0 < x < 1,\,x\,{\log _e}x < 0,{\text{ and for }}x > 1,\,x\,{\log _e}x > 0$$
Also $$x\,{\log _e}x = 0{\text{ or }}x = 1$$
Further $$\frac{{dy}}{{dx}} = 0 \Rightarrow 1 + {\log _e}x = 0{\text{ or }}x = \frac{1}{e},$$ which is point of minima.
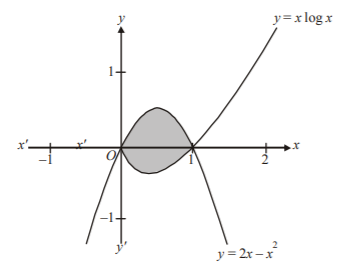
Required area
$$\eqalign{ & = \int\limits_0^1 {\left( {2x - 2{x^2}} \right)dx} - \int\limits_0^1 {x\,\log \,x\,dx} \cr & = \left[ {{x^2} - \frac{{2{x^3}}}{3}} \right]_0^1 - \left[ {\frac{{{x^2}}}{2}\log \,x - \frac{{{x^2}}}{4}} \right]_0^1 \cr & = \left( {1 - \frac{2}{3}} \right) - \left[ {0 - \frac{1}{4} - \frac{1}{2}\mathop {\lim }\limits_{x \to 0} {x^2}\log \,x} \right] \cr & = \frac{1}{3} + \frac{1}{4} \cr & = \frac{7}{{12}} \cr} $$
Curve tracing, $$y = x\,{\log _e}x$$
Clearly $$x > 0,$$
For $$0 < x < 1,\,x\,{\log _e}x < 0,{\text{ and for }}x > 1,\,x\,{\log _e}x > 0$$
Also $$x\,{\log _e}x = 0{\text{ or }}x = 1$$
Further $$\frac{{dy}}{{dx}} = 0 \Rightarrow 1 + {\log _e}x = 0{\text{ or }}x = \frac{1}{e},$$ which is point of minima.

Required area
$$\eqalign{ & = \int\limits_0^1 {\left( {2x - 2{x^2}} \right)dx} - \int\limits_0^1 {x\,\log \,x\,dx} \cr & = \left[ {{x^2} - \frac{{2{x^3}}}{3}} \right]_0^1 - \left[ {\frac{{{x^2}}}{2}\log \,x - \frac{{{x^2}}}{4}} \right]_0^1 \cr & = \left( {1 - \frac{2}{3}} \right) - \left[ {0 - \frac{1}{4} - \frac{1}{2}\mathop {\lim }\limits_{x \to 0} {x^2}\log \,x} \right] \cr & = \frac{1}{3} + \frac{1}{4} \cr & = \frac{7}{{12}} \cr} $$