Question
The area of the region bounded by the parabola $${\left( {y - 2} \right)^2} = x - 1,$$ the tangent of the parabola at the point $$\left( {2,\,3} \right)$$ and the $$x$$-axis is :
A.
6
B.
9
C.
12
D.
3
Answer :
9
Solution :
The given parabola is $${\left( {y - 2} \right)^2} = x - 1$$
Vertex $$\left( {1,\,2} \right)$$ and it meets $$x$$-axis at $$\left( {5,\,0} \right)$$
Also it gives $${y^2} - 4y - x + 5 = 0$$
So, that equation of tangent to the parabola at $$\left( {2,\,3} \right)$$ is
$$\eqalign{ & y.3 - 2\left( {y + 3} \right) - \frac{1}{2}\left( {x + 2} \right) + 5 = 0 \cr & {\text{or }}x - 2y + 4 = 0\,\,{\text{which meets }}x{\text{ - axis at }}\left( { - 4,\,0} \right) \cr} $$
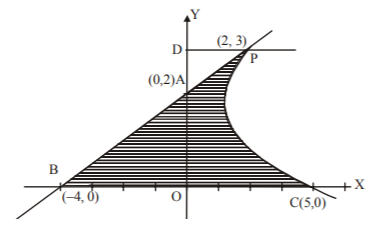
In the figure shaded area is the required area.
Let us draw $$PD$$ perpendicular to $$y$$-axis.
Then required area
$$\eqalign{ & = Ar\left( {\Delta BOA} \right) + Ar\left( {OCPD} \right) - Ar\left( {\Delta APD} \right) \cr & = \frac{1}{2} \times 4 \times 2 + \int_0^3 {x\,dy - \frac{1}{2} \times 2 \times 1} \cr & = 3 + \int_0^3 {{{\left( {y - 2} \right)}^2} + 1\,dy} \cr & = 3 + \left[ {\frac{{{{\left( {y - 2} \right)}^3}}}{3} + y} \right]_0^3 \cr & = 3 + \left[ {\frac{1}{3} + 3 + \frac{8}{3}} \right] \cr & = 3 + 6 \cr & = 9\,{\text{sq}}{\text{. units}} \cr} $$
The given parabola is $${\left( {y - 2} \right)^2} = x - 1$$
Vertex $$\left( {1,\,2} \right)$$ and it meets $$x$$-axis at $$\left( {5,\,0} \right)$$
Also it gives $${y^2} - 4y - x + 5 = 0$$
So, that equation of tangent to the parabola at $$\left( {2,\,3} \right)$$ is
$$\eqalign{ & y.3 - 2\left( {y + 3} \right) - \frac{1}{2}\left( {x + 2} \right) + 5 = 0 \cr & {\text{or }}x - 2y + 4 = 0\,\,{\text{which meets }}x{\text{ - axis at }}\left( { - 4,\,0} \right) \cr} $$

In the figure shaded area is the required area.
Let us draw $$PD$$ perpendicular to $$y$$-axis.
Then required area
$$\eqalign{ & = Ar\left( {\Delta BOA} \right) + Ar\left( {OCPD} \right) - Ar\left( {\Delta APD} \right) \cr & = \frac{1}{2} \times 4 \times 2 + \int_0^3 {x\,dy - \frac{1}{2} \times 2 \times 1} \cr & = 3 + \int_0^3 {{{\left( {y - 2} \right)}^2} + 1\,dy} \cr & = 3 + \left[ {\frac{{{{\left( {y - 2} \right)}^3}}}{3} + y} \right]_0^3 \cr & = 3 + \left[ {\frac{1}{3} + 3 + \frac{8}{3}} \right] \cr & = 3 + 6 \cr & = 9\,{\text{sq}}{\text{. units}} \cr} $$