Question
The area (in sq. units) of the region $$\left\{ {\left( {x,\,y} \right):{y^2} \geqslant 2x\,\,{\text{and}}\,{x^2} + {y^2} \leqslant 4x,\,x \geqslant 0,\,y \geqslant 0} \right\}$$ is :
A.
$$\pi - \frac{{4\sqrt 2 }}{3}$$
B.
$$\frac{\pi }{2} - \frac{{2\sqrt 2 }}{3}$$
C.
$$\pi - \frac{4}{3}$$
D.
$$\pi - \frac{8}{3}$$
Answer :
$$\pi - \frac{8}{3}$$
Solution :
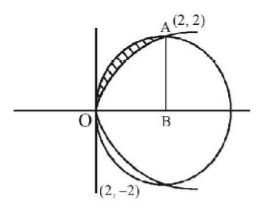
Points of intersection of the two curves are $$\left( {0,\,0} \right),\,\left( {2,\,2} \right)$$ and $$\left( {2,\, - 2} \right)$$
Area $$=$$ Area $$\left( {OAB} \right) - $$ area under parabola $$\left( {0{\text{ to }}2} \right)$$
$$\eqalign{ & = \frac{{\pi \times {{\left( 2 \right)}^2}}}{4} - \int\limits_0^2 {\sqrt 2 } \sqrt x \,dx \cr & = \pi - \frac{8}{3} \cr} $$

Points of intersection of the two curves are $$\left( {0,\,0} \right),\,\left( {2,\,2} \right)$$ and $$\left( {2,\, - 2} \right)$$
Area $$=$$ Area $$\left( {OAB} \right) - $$ area under parabola $$\left( {0{\text{ to }}2} \right)$$
$$\eqalign{ & = \frac{{\pi \times {{\left( 2 \right)}^2}}}{4} - \int\limits_0^2 {\sqrt 2 } \sqrt x \,dx \cr & = \pi - \frac{8}{3} \cr} $$