Question
The area enclosed by the curves $$y = \sin \,x + \cos \,x$$ and $$y = \left| {\cos \,x - \sin \,x} \right|$$ over the interval $$\left[ {0,\,\frac{\pi }{2}} \right]$$ is-
A.
$$4\left( {\sqrt 2 - 1} \right)$$
B.
$$2\sqrt 2 \left( {\sqrt 2 - 1} \right)$$
C.
$$2\left( {\sqrt 2 + 1} \right)$$
D.
$$2\sqrt 2 \left( {\sqrt 2 + 1} \right)$$
Answer :
$$2\sqrt 2 \left( {\sqrt 2 - 1} \right)$$
Solution :
The rough graph of $$y = \sin \,x + \cos \,x$$ and $$y = \left| {\cos \,x - \sin \,x} \right|$$ suggest the required area is
$$ = \int_0^{\frac{\pi }{2}} {\left[ {\left( {\sin \,x + \cos \,x} \right) - \left| {\cos \,x - \sin \,x} \right|} \right]} dx$$
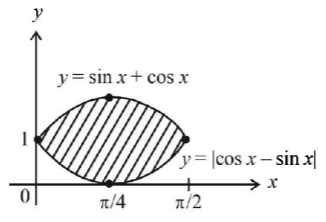
$$\eqalign{ & = \int_0^{\frac{\pi }{4}} {2\,\sin \,x\,dx} + \int_{\frac{\pi }{4}}^{\frac{\pi }{2}} {2\,\cos \,x\,dx} \cr & = 2\left[ {\left( { - \cos \,x} \right)_0^{\frac{\pi }{4}} + \left( {\sin \,x} \right)_{\frac{\pi }{4}}^{\frac{\pi }{2}}} \right] \cr & = 2\sqrt 2 \left( {\sqrt 2 - 1} \right) \cr} $$
The rough graph of $$y = \sin \,x + \cos \,x$$ and $$y = \left| {\cos \,x - \sin \,x} \right|$$ suggest the required area is
$$ = \int_0^{\frac{\pi }{2}} {\left[ {\left( {\sin \,x + \cos \,x} \right) - \left| {\cos \,x - \sin \,x} \right|} \right]} dx$$

$$\eqalign{ & = \int_0^{\frac{\pi }{4}} {2\,\sin \,x\,dx} + \int_{\frac{\pi }{4}}^{\frac{\pi }{2}} {2\,\cos \,x\,dx} \cr & = 2\left[ {\left( { - \cos \,x} \right)_0^{\frac{\pi }{4}} + \left( {\sin \,x} \right)_{\frac{\pi }{4}}^{\frac{\pi }{2}}} \right] \cr & = 2\sqrt 2 \left( {\sqrt 2 - 1} \right) \cr} $$