Question
The area enclosed between the curves $$y = {\log _e}\left( {x + e} \right),\,x = {\log _e}\left( {\frac{1}{y}} \right),$$ and the $$x$$-axis is :
A.
2 sq. units
B.
1 sq. unit
C.
4 sq. units
D.
None of these
Answer :
2 sq. units
Solution :
$$y = {\log _e}\left( {x + e} \right),\,x = {\log _e}\left( {\frac{1}{y}} \right),{\text{ or }}y = {e^{ - x}}$$
For $$y = {\log _e}\left( {x + e} \right),$$ shift the graph of $$y = {\log _e}x,\,\,e$$ units to the left hand side.
Required area
$$\eqalign{ & = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)} dx + \int\limits_0^\infty {{e^{ - x}}dx} \cr & = \left| {x\,{{\log }_e}\left( {x + e} \right)} \right|_{1 - e}^0 - \int\limits_{1 - e}^0 {\frac{x}{{x + e}}} dx - \left| {{e^{ - x}}} \right|_0^\infty \cr & = \int\limits_0^{1 - e} {\left( {1 - \frac{e}{{x + e}}} \right)dx - {e^{ - \infty }}} + {e^0} \cr & = \left| {x - e\,\log \left( {x + e} \right)} \right|_0^{1 - e} - 0 + 1 \cr & = 1 - e + e\,\log \,e + 1 \cr & = 2{\text{ sq}}{\text{. units}} \cr} $$
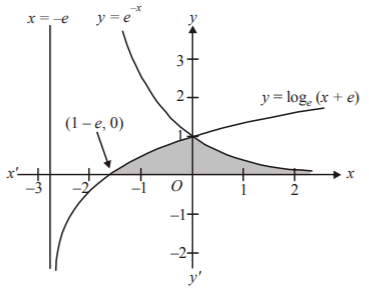
$$y = {\log _e}\left( {x + e} \right),\,x = {\log _e}\left( {\frac{1}{y}} \right),{\text{ or }}y = {e^{ - x}}$$
For $$y = {\log _e}\left( {x + e} \right),$$ shift the graph of $$y = {\log _e}x,\,\,e$$ units to the left hand side.
Required area
$$\eqalign{ & = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)} dx + \int\limits_0^\infty {{e^{ - x}}dx} \cr & = \left| {x\,{{\log }_e}\left( {x + e} \right)} \right|_{1 - e}^0 - \int\limits_{1 - e}^0 {\frac{x}{{x + e}}} dx - \left| {{e^{ - x}}} \right|_0^\infty \cr & = \int\limits_0^{1 - e} {\left( {1 - \frac{e}{{x + e}}} \right)dx - {e^{ - \infty }}} + {e^0} \cr & = \left| {x - e\,\log \left( {x + e} \right)} \right|_0^{1 - e} - 0 + 1 \cr & = 1 - e + e\,\log \,e + 1 \cr & = 2{\text{ sq}}{\text{. units}} \cr} $$
