Question
The area enclosed between the curve $$y = {\log _e}\left( {x + e} \right)$$ and the coordinate axes is-
A.
$$1$$
B.
$$2$$
C.
$$3$$
D.
$$4$$
Answer :
$$1$$
Solution :
The graph of the curve $$y = {\log _e}\left( {x + e} \right)$$ is as shown in the figure
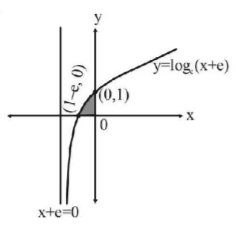
$$\eqalign{ & {\text{Required area}}\,{\text{:}} \cr & A = \int\limits_{1 - e}^0 {y\,dx} = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)dx} \cr & {\text{Put}}\,x + e = t\,\, \Rightarrow dx = dt \cr & {\text{Also}}\,x = 1 - e,\,\,t = 1 \cr & {\text{At}}\,x = 0,\,t = e \cr & \therefore A = \int\limits_1^e {{{\log }_e}t\,dt} = \left[ {t\,{{\log }_e}t - t} \right]_1^e \cr & e - e - 0 + 1 = 1 \cr} $$
Hence the required area is 1 square unit.
The graph of the curve $$y = {\log _e}\left( {x + e} \right)$$ is as shown in the figure

$$\eqalign{ & {\text{Required area}}\,{\text{:}} \cr & A = \int\limits_{1 - e}^0 {y\,dx} = \int\limits_{1 - e}^0 {{{\log }_e}\left( {x + e} \right)dx} \cr & {\text{Put}}\,x + e = t\,\, \Rightarrow dx = dt \cr & {\text{Also}}\,x = 1 - e,\,\,t = 1 \cr & {\text{At}}\,x = 0,\,t = e \cr & \therefore A = \int\limits_1^e {{{\log }_e}t\,dt} = \left[ {t\,{{\log }_e}t - t} \right]_1^e \cr & e - e - 0 + 1 = 1 \cr} $$
Hence the required area is 1 square unit.