The area bounded by the curves $$y = \ln \,x,\,y = \ln \left| x \right|,\,y = \left| {\ln \,x} \right|$$      and $$y = \left| {\ln \left| x \right|} \right|$$   is-

Solution :
First we draw each curve as separate graph

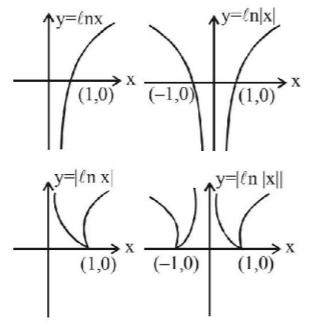
NOTE : Graph of $$y = \left| {f\left( x \right)} \right|$$   can be obtained from the graph of the curve $$y = f\left( x \right)$$   by drawing the mirror image of the portion of the graph below $$x$$-axis, with respect to $$x$$-axis.
Clearly the bounded area is as shown in the following figure.

$$\eqalign{ & {\text{Required area}}\, = 4\int\limits_0^1 {\left( { - \ell nx} \right)dx} \cr & = - 4\left[ {x\,\ell n\,x - x} \right]_0^1 \cr & = 4\,{\text{sq}}{\text{. units}} \cr} $$