Question
The angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at distances $$49\,m$$ and $$36\,m$$ are $${43^ \circ }$$ and $${47^ \circ }$$ respectively. What is the height of the tower ?
A.
$$40\,m$$
B.
$$42\,m$$
C.
$$45\,m$$
D.
$$47\,m$$
Answer :
$$42\,m$$
Solution :
$$\eqalign{ & AB = h\left( {{\text{height of the tower}}} \right) \cr & BD = 36\,m;\,\,BC = 49\,m \cr & \angle D = {47^ \circ };\,\,\angle C = {43^ \circ } \cr} $$
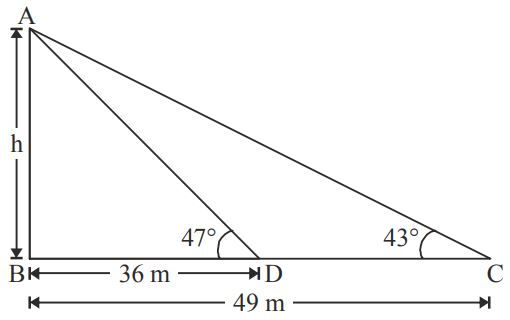
$$\eqalign{ & {\text{Now, in }}\Delta \,ABD, \cr & \tan {47^ \circ } = \frac{h}{{36\,m}}\,\,\,\,.....\left( {\text{i}} \right) \cr & {\text{and in }}\Delta \,ABC,\tan {43^ \circ } = \frac{h}{{49\,m}} \cr & \tan \left( {{{90}^ \circ } - {{47}^ \circ }} \right) = \frac{h}{{49}} \cr & \therefore \cot {47^ \circ } = \frac{h}{{49}}\,\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
Multiplying equations (i) and (ii)
$$\eqalign{ & \tan {47^ \circ } \cdot \cot {47^ \circ } = \frac{h}{{36}} \times \frac{h}{{49}} = 1 = \frac{{{h^2}}}{{36 \times 49}} \cr & h = 6 \times 7 = 42\,m \cr} $$
$$\therefore $$ Option $$\left( {B} \right)$$ is correct.
$$\eqalign{ & AB = h\left( {{\text{height of the tower}}} \right) \cr & BD = 36\,m;\,\,BC = 49\,m \cr & \angle D = {47^ \circ };\,\,\angle C = {43^ \circ } \cr} $$

$$\eqalign{ & {\text{Now, in }}\Delta \,ABD, \cr & \tan {47^ \circ } = \frac{h}{{36\,m}}\,\,\,\,.....\left( {\text{i}} \right) \cr & {\text{and in }}\Delta \,ABC,\tan {43^ \circ } = \frac{h}{{49\,m}} \cr & \tan \left( {{{90}^ \circ } - {{47}^ \circ }} \right) = \frac{h}{{49}} \cr & \therefore \cot {47^ \circ } = \frac{h}{{49}}\,\,\,\,.....\left( {{\text{ii}}} \right) \cr} $$
Multiplying equations (i) and (ii)
$$\eqalign{ & \tan {47^ \circ } \cdot \cot {47^ \circ } = \frac{h}{{36}} \times \frac{h}{{49}} = 1 = \frac{{{h^2}}}{{36 \times 49}} \cr & h = 6 \times 7 = 42\,m \cr} $$
$$\therefore $$ Option $$\left( {B} \right)$$ is correct.