Temperature difference of $$120{\,^ \circ }C$$  is maintained between two ends of a uniform rod $$AB$$  of length $$2\,L.$$  Another bent rod $$PQ,$$  of same cross - section as $$AB$$  and length $$\frac{{3\,L}}{2},$$  is connected across $$AB$$  (See figure). In steady state, temperature difference between $$P$$ and $$Q$$ will be close to :

Solution :

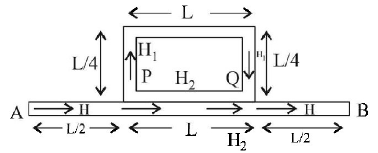
At, $$P$$
$$\eqalign{ & H = {H_1} + {H_{2s}} \cr & \frac{{kA\left( {{T_A} - {T_P}} \right)}}{{\frac{L}{2}}} \cr & = \frac{{kA\left( {{T_P} - {T_Q}} \right)}}{{\frac{{3L}}{2}}} + \frac{{kA\left( {{T_P} - {T_Q}} \right)}}{L} \cr & \therefore \,\,2\left( {{T_A} - {T_P}} \right) = \frac{2}{3}\left( {{T_P} - {T_Q}} \right) + \left( {{T_P} - {T_Q}} \right) \cr & \therefore \,\,2\left( {{T_A} - {T_P}} \right) = \frac{5}{3}\left( {{T_P} - {T_Q}} \right)\,\,\,.....\left( {\text{i}} \right) \cr & {\text{At, }}Q \cr & {H_1} + {H_2} = H \cr & \therefore \,\,\frac{{kA\left( {{T_P} - {T_Q}} \right)}}{{\frac{{3L}}{2}}} + \frac{{kA\left( {{T_P} - {T_Q}} \right)}}{L} \cr & = \frac{{kA\left( {{T_Q} - {T_B}} \right)}}{{\frac{L}{2}}}\,\,\,\,\,\,.....\left( {{\text{ii}}} \right) \cr & \therefore \,\,2\left( {{T_Q} - {T_P}} \right) = \frac{5}{3}\left( {{T_P} - {T_Q}} \right) \cr} $$
From (i) & (ii)
$$\eqalign{ & 2\left( {{T_A} - {T_P}} \right) + 2\left( {{T_Q} - {T_B}} \right) = \frac{{10}}{3}\left( {{T_P} - {T_Q}} \right) \cr & {T_A} - {T_B} = \frac{8}{3}\left( {{T_P} - {T_Q}} \right) \cr & \therefore \,\,{T_P} - {T_Q} = \frac{3}{8} \times 120 \cr & = 45{\,^ \circ }C \cr} $$