Question
Tangent to the curve $$y = {x^2} + 6$$ at a point (1, 7) touches the circle $${x^2} + {y^2} + 16x + 12y + c = 0$$ at a point $$Q.$$ Then the coordinates of $$Q$$ are-
A.
$$\left( { - 6,\, - 11} \right)$$
B.
$$\left( { - 9,\, - 13} \right)$$
C.
$$\left( { - 10,\, - 15} \right)$$
D.
$$\left( { - 6,\, - 7} \right)$$
Answer :
$$\left( { - 6,\, - 7} \right)$$
Solution :
The given curve is $$y = {x^2} + 6$$
Equation of tangent at $$\left( {1,\,7} \right)$$ is
$$\eqalign{ & \frac{1}{2}\left( {y + 7} \right) = x.1 + 6 \cr & \Rightarrow 2x - y + 5 = 0.....(1) \cr} $$
As given this tangent (1) touches the circle $${x^2} + {y^2} + 16x + 12y + c = 0$$ at $$Q$$
Centre of circle $$ = \left( { - 8,\, - 6} \right).$$
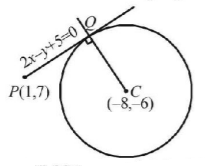
Then equation of $$CQ$$ which is perpendicular to (1) and passes through $$\left( { - 8,\, - 6} \right)$$ is $$y + 6 = - \frac{1}{2}\left( {x + 8} \right)$$
$$ \Rightarrow x + 2y + 20 = 0.....(2)$$
Now $$Q$$ is points of intersection of (1) and (2)
$$\therefore $$ Solving equation (1) & (2) we get
$$x=-6,\,\,y=-7$$
$$\therefore $$ Required points is $$\left( { - 6,\, - 7} \right)$$
The given curve is $$y = {x^2} + 6$$
Equation of tangent at $$\left( {1,\,7} \right)$$ is
$$\eqalign{ & \frac{1}{2}\left( {y + 7} \right) = x.1 + 6 \cr & \Rightarrow 2x - y + 5 = 0.....(1) \cr} $$
As given this tangent (1) touches the circle $${x^2} + {y^2} + 16x + 12y + c = 0$$ at $$Q$$
Centre of circle $$ = \left( { - 8,\, - 6} \right).$$

Then equation of $$CQ$$ which is perpendicular to (1) and passes through $$\left( { - 8,\, - 6} \right)$$ is $$y + 6 = - \frac{1}{2}\left( {x + 8} \right)$$
$$ \Rightarrow x + 2y + 20 = 0.....(2)$$
Now $$Q$$ is points of intersection of (1) and (2)
$$\therefore $$ Solving equation (1) & (2) we get
$$x=-6,\,\,y=-7$$
$$\therefore $$ Required points is $$\left( { - 6,\, - 7} \right)$$