Question
Suppose $$f\left( x \right) = {\left( {x + 1} \right)^2}$$ for $$x \geqslant - 1.$$ If $$g\left( x \right)$$ is the function whose graph is the reflection of the graph of $$f\left( x \right)$$ with respect to the line $$y = x,$$ then $$g\left( x \right)$$ equals
A.
$$ - \sqrt {x - 1} ,x \geqslant 0$$
B.
$$\frac{1}{{{{\left( {x + 1} \right)}^2}}},x > - 1$$
C.
$$\sqrt {x + 1} ,x \geqslant - 1$$
D.
$$\sqrt {x - 1} ,x \geqslant 0$$
Answer :
$$\sqrt {x - 1} ,x \geqslant 0$$
Solution :
Given that f $$f\left( x \right) = {\left( {x + 1} \right)^2},x \geqslant - 1$$
Now if $$g\left( x \right)$$ is the reflection of $$f\left( x \right)$$ in the line $$y = x$$ then it can be obtained by interchanging $$x$$ and $$y$$ in $$f\left( x \right)$$
i.e., $$y = {\left( {x + 1} \right)^2}$$ changes to $$x = {\left( {y + 1} \right)^2}$$
$$\eqalign{ & \Rightarrow y + 1 = \sqrt x \cr & \left[ {y + 1 \ne - \sqrt x ,\,{\text{since}}\,y \geqslant - 1\,{\text{as}}\,{\text{in}}\,{\text{figure}}.} \right. \cr & \Rightarrow y = \sqrt x - 1\,{\text{defined}}\,\forall x \geqslant 0 \cr} $$
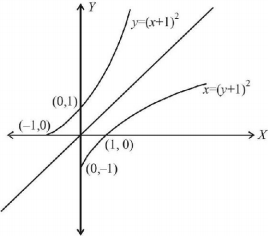
$$\therefore g\left( x \right) = \sqrt x - 1\,\forall x \geqslant 0$$
Given that f $$f\left( x \right) = {\left( {x + 1} \right)^2},x \geqslant - 1$$
Now if $$g\left( x \right)$$ is the reflection of $$f\left( x \right)$$ in the line $$y = x$$ then it can be obtained by interchanging $$x$$ and $$y$$ in $$f\left( x \right)$$
i.e., $$y = {\left( {x + 1} \right)^2}$$ changes to $$x = {\left( {y + 1} \right)^2}$$
$$\eqalign{ & \Rightarrow y + 1 = \sqrt x \cr & \left[ {y + 1 \ne - \sqrt x ,\,{\text{since}}\,y \geqslant - 1\,{\text{as}}\,{\text{in}}\,{\text{figure}}.} \right. \cr & \Rightarrow y = \sqrt x - 1\,{\text{defined}}\,\forall x \geqslant 0 \cr} $$

$$\therefore g\left( x \right) = \sqrt x - 1\,\forall x \geqslant 0$$