Question
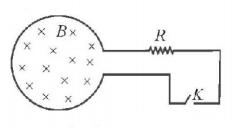
Shown in the figure is a circular loop of radius $$r$$ and resistance $$R.$$ A variable magnetic field of induction $$B = {B_0}{e^{ - t}}$$ is established inside the coil. If the key $$\left( K \right)$$ is closed, the electrical power developed right after closing the switch is equal to
Shown in the figure is a circular loop of radius $$r$$ and resistance $$R.$$ A variable magnetic field of induction $$B = {B_0}{e^{ - t}}$$ is established inside the coil. If the key $$\left( K \right)$$ is closed, the electrical power developed right after closing the switch is equal to
A.
$$\frac{{B_0^2\pi {r^2}}}{R}$$
B.
$$\frac{{{B_0}10{r^3}}}{R}$$
C.
$$\frac{{B_0^2{\pi ^2}{r^4}R}}{5}$$
D.
$$\frac{{B_0^2{\pi ^2}{r^4}}}{R}$$
Answer :
$$\frac{{B_0^2{\pi ^2}{r^4}}}{R}$$
Solution :
$$\eqalign{ & e = - \frac{{d\phi }}{{dt}} - A\frac{{dB}}{{dt}} = - \pi {r^2}\frac{d}{{dt}}\left( {{B_0}{e^{ - t}}} \right) = \pi {r^2}{B_0}{e^{ - t}} \cr & {\text{At}}\,\,t = 0,e = \pi {r^2}{B_0},P = \frac{{{e^2}}}{R} = \frac{{{{\left( {\pi {r^2}{B_0}} \right)}^2}}}{R} = \frac{{{\pi ^2}{r^4}B_0^2}}{R} \cr} $$
$$\eqalign{ & e = - \frac{{d\phi }}{{dt}} - A\frac{{dB}}{{dt}} = - \pi {r^2}\frac{d}{{dt}}\left( {{B_0}{e^{ - t}}} \right) = \pi {r^2}{B_0}{e^{ - t}} \cr & {\text{At}}\,\,t = 0,e = \pi {r^2}{B_0},P = \frac{{{e^2}}}{R} = \frac{{{{\left( {\pi {r^2}{B_0}} \right)}^2}}}{R} = \frac{{{\pi ^2}{r^4}B_0^2}}{R} \cr} $$
