Question
$$PQR$$ is a triangular park with $$PQ = PR = 200 m.$$ A. T. V. tower stands at the mid - point of $$QR.$$ If the angles of elevation of the top of the tower at $$P, Q$$ and $$R$$ are respectively 45°, 30° and 30°, then the height of the tower (in $$m$$ ) is:
A.
50
B.
$$100\sqrt 3 $$
C.
$$50\sqrt 2 $$
D.
100
Answer :
100
Solution :
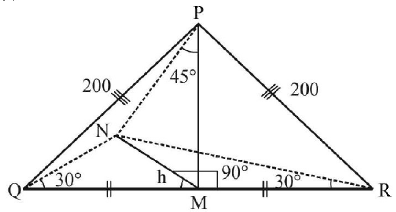
Let height of tower $$MN = h$$
In $$\Delta QMN$$ we have
$$\eqalign{ & \tan {30^ \circ } = \frac{{MN}}{{QM}} \cr & \therefore \,\,QM = \sqrt 3 \,h = MR\,\,\,.....\left( 1 \right) \cr & {\text{Now in }}\Delta MNP \cr & MN = PM\,\,\,\,\,\,\,.....\left( 2 \right) \cr & {\text{In }}\Delta PMQ\,\,{\text{we have :}} \cr & MP = \sqrt {{{\left( {200} \right)}^2} - {{\left( {\sqrt 3 \,h} \right)}^2}} \cr & \therefore \,\,{\text{From }}\left( 2 \right),{\text{ we get :}} \cr & \sqrt {{{\left( {200} \right)}^2} - {{\left( {\sqrt 3 \,h} \right)}^2}} = h \cr & \Rightarrow \,\,h = 100\,m \cr} $$

Let height of tower $$MN = h$$
In $$\Delta QMN$$ we have
$$\eqalign{ & \tan {30^ \circ } = \frac{{MN}}{{QM}} \cr & \therefore \,\,QM = \sqrt 3 \,h = MR\,\,\,.....\left( 1 \right) \cr & {\text{Now in }}\Delta MNP \cr & MN = PM\,\,\,\,\,\,\,.....\left( 2 \right) \cr & {\text{In }}\Delta PMQ\,\,{\text{we have :}} \cr & MP = \sqrt {{{\left( {200} \right)}^2} - {{\left( {\sqrt 3 \,h} \right)}^2}} \cr & \therefore \,\,{\text{From }}\left( 2 \right),{\text{ we get :}} \cr & \sqrt {{{\left( {200} \right)}^2} - {{\left( {\sqrt 3 \,h} \right)}^2}} = h \cr & \Rightarrow \,\,h = 100\,m \cr} $$