Question
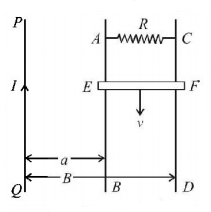
$$PQ$$ is an infinite current carrying conductor. $$AB$$ and $$CD$$ are smooth conducting rods on which a conductor $$EF$$ moves with constant velocity $$v$$ as shown. The force needed to maintain constant speed of $$EF$$ is
$$PQ$$ is an infinite current carrying conductor. $$AB$$ and $$CD$$ are smooth conducting rods on which a conductor $$EF$$ moves with constant velocity $$v$$ as shown. The force needed to maintain constant speed of $$EF$$ is
A.
$$\frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
B.
$${\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{a}{b}} \right)} \right]^2}\frac{1}{{vR}}$$
C.
$${\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}\frac{v}{R}$$
D.
$$\frac{v}{R}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{a}{b}} \right)} \right]^2}$$
Answer :
$$\frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
Solution :
Induced emf $$ = \int\limits_a^b {Bv} dx = \int\limits_a^b {\frac{{{\mu _0}I}}{{2\pi x}}} vdx$$
$$ \Rightarrow $$ Induced emf $$ = \frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)$$
$$ \Rightarrow $$ Power dissipated $$ = \frac{{{E^2}}}{R}$$
Also, power $$ = F.v \Rightarrow F = \frac{{{E^2}}}{{vR}}$$
$$ \Rightarrow F = \frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
Induced emf $$ = \int\limits_a^b {Bv} dx = \int\limits_a^b {\frac{{{\mu _0}I}}{{2\pi x}}} vdx$$
$$ \Rightarrow $$ Induced emf $$ = \frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)$$
$$ \Rightarrow $$ Power dissipated $$ = \frac{{{E^2}}}{R}$$
Also, power $$ = F.v \Rightarrow F = \frac{{{E^2}}}{{vR}}$$
$$ \Rightarrow F = \frac{1}{{vR}}{\left[ {\frac{{{\mu _0}Iv}}{{2\pi }}\ln \left( {\frac{b}{a}} \right)} \right]^2}$$
