Point masses $${m_1}$$ and $${m_2}$$ are placed at the opposite ends of a rigid rod of length $$L$$ and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point $$P$$ on this rod through which the axis should pass, so that the work required to set the rod rotating with angular velocity $${\omega _0}$$ is minimum, is given by

Solution :

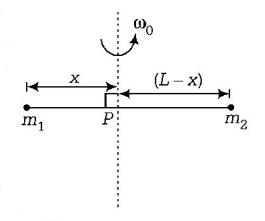
As two point masses $${m_1}$$ and $${m_2}$$ are placed at opposite ends of a rigid rod of length $$L$$ and negligible mass as shown in figure. Total moment of inertia of the rod
$$\eqalign{ & I = {m_1}{x^2} + {m_2}{\left( {L - x} \right)^2} \cr & I = {m_1}{x^2} + {m_2}{L^2} + {m_2}{x^2} - 2{m_2}Lx \cr} $$
As, $$I$$ is minimum i.e.
$$\eqalign{ & \frac{{dI}}{{dx}} = 2{m_1}x + 0 + 2x{m_2} - 2{m_2}L = 0 \cr & \Rightarrow x\left( {2{m_1} + 2{m_2}} \right) = 2{m_2}L \cr & \Rightarrow x = \frac{{{m_2}L}}{{{m_1} + {m_2}}} \cr} $$
When $$I$$ is minimum, then work done on rotating a rod $$\frac{1}{2}I{\omega ^2}$$  with angular velocity $${\omega _0}$$ will be minimum.
Shortcut Way
The position of point $$P$$ on rod through which the axis should pass, so that the work required to set the rod rotating with minimum angular velocity $${\omega _0}$$ is their centre of mass, we have
$${m_1}x = {m_2}\left( {L - x} \right) \Rightarrow x = \frac{{{m_2}L}}{{{m_1} + {m_2}}}$$