51. The equation of a wave is given by $$y = a\sin \left( {100t - \frac{x}{{10}}} \right),$$ where $$x$$ and $$y$$ are in metre and $$t$$ in second, then velocity of wave is
A
$$0.1\,m/s$$
B
$$10\,m/s$$
C
$$100\,m/s$$
D
$$1000\,m/s$$
Answer :
$$1000\,m/s$$
52. Two tones of frequencies $${n_1}$$ and $${n_2}$$ are sounded together. The beats can be heard distinctly when
A
$$10 < \left( {{n_1} - {n_2}} \right) < 20$$
B
$$5 < \left( {{n_1} - {n_2}} \right) > 20$$
C
$$5 < \left( {{n_1} - {n_2}} \right) < 20$$
D
$$0 < \left( {{n_1} - {n_2}} \right) < 10$$
Answer :
$$0 < \left( {{n_1} - {n_2}} \right) < 10$$
53. A stretched wire $$60\,cm$$ long is vibrating with its fundamental frequency of $$256\,Hz.$$ If the length of the wire is decreased to $$15\,cm$$ and the tension remains the same. Then the fundamental frequency of the vibration of the wire will be
A
1024
B
572
C
256
D
64
Answer :
1024
54. A stretched string resonates with tuning fork of frequency $$512\,Hz$$ when length of the string is $$0.5\,m.$$ The length of the string required to vibrate resonantly with a tuning fork of frequency $$256\,Hz$$ would be
A
$$0.25\,m$$
B
$$0.5\,m$$
C
$$1\,m$$
D
$$2\,m$$
Answer :
$$1\,m$$
55. A source producing sound of frequency $$170\,Hz$$ is approaching a stationary observer with a velocity $$17\,m{s^{ - 1}}.$$ The apparent change in the wavelength of sound heard by the observer is (speed of sound in air $$ = 340\,m{s^{ - 1}}$$ )
A
$$0.1\,m$$
B
$$0.2\,m$$
C
$$0.4\,m$$
D
$$0.5\,m$$
Answer :
$$0.1\,m$$
56.
A transverse sinusoidal wave moves along a string in the positive $$x$$-direction at a speed of $$10\,cm/s.$$ The wavelength of the wave is $$0.5\,m$$ and its amplitude is $$10\,cm.$$ At a particular time $$t,$$ the snap-shot of the wave is shown in figure. The velocity of point $$P$$ when its displacement is $$5\,cm$$ is

A
$$\frac{{\sqrt 3 \pi }}{{50}}\hat j\,m/s$$
B
$$ - \frac{{\sqrt 3 \pi }}{{50}}\hat j\,m/s$$
C
$$\frac{{\sqrt 3 \pi }}{{50}}\hat i\,m/s$$
D
$$ - \frac{{\sqrt 3 \pi }}{{50}}\hat i\,m/s$$
Answer :
$$\frac{{\sqrt 3 \pi }}{{50}}\hat j\,m/s$$
57. Two vibrating tuning forks produce progressive waves given by $${Y_1} = 4\sin 500\,\pi t$$ and $${Y_2} = 2\sin 506\,\pi t.$$ Number of beats produced per minute is
A
360
B
180
C
60
D
3
Answer :
180
58. Which of the following equation represents a wave?
A
$$y = a\sin \omega t$$
B
$$y = a\cos kx$$
C
$$y = a\sin \left( {\omega t - bx + c} \right)$$
D
$$y = a\sin \left( {\omega t - kx} \right)$$
Answer :
$$y = a\sin \left( {\omega t - kx} \right)$$
59.
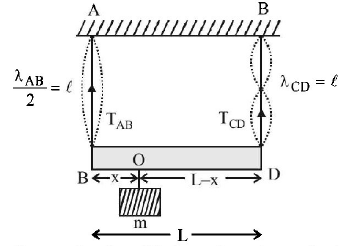
A massless rod of length $$L$$ is suspended by two identical strings $$AB$$ and $$CD$$ of equal length. A block of mass $$m$$ is suspended from point $$O$$ such that $$BO$$ is equal to $$'x'.$$ Further it is observed that the frequency of $${1^{st}}$$ harmonic in $$AB$$ is equal to $${2^{nd}}$$ harmonic frequency in $$CD. $$ $$'x’$$ is

A
$$\frac{L}{5}$$
B
$$\frac{4\,L}{5}$$
C
$$\frac{3\,L}{4}$$
D
$$\frac{L}{4}$$
Answer :
$$\frac{L}{5}$$
60.
A transverse wave is represented by the equation
$$y = {y_0}\sin \frac{{2\pi }}{\lambda }\left( {vt - x} \right)$$
For what value of $$\lambda $$ is the maximum particle velocity equal to two times the wave velocity ?
A
$$\lambda = 2\,\pi {y_0}$$
B
$$\lambda = \frac{{\pi {y_0}}}{3}$$
C
$$\lambda = \frac{{\pi {y_0}}}{2}$$
D
$$\lambda = \pi {y_0}$$
Answer :
$$\lambda = \pi {y_0}$$