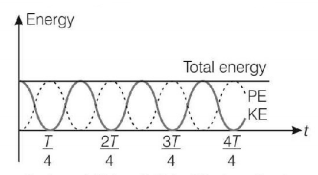
71.
The total energy of a particle, executing simple harmonic motion is:
(Where $$x$$ is the displacement from the mean position, hence total energy is independent of $$x.$$)
A
independent of $$x$$
B
$$ \propto {x^2}$$
C
$$ \propto x$$
D
$$ \propto {x^{\frac{1}{2}}}$$
Answer :
independent of $$x$$
72.
The displacement of a particle in simple harmonic motion in one time period is
[$$A$$ = amplitude]
A
$$A$$
B
$$2\,A$$
C
$$4\,A$$
D
Zero
Answer :
Zero
73. A simple harmonic motion has an amplitude $$A$$ and time period $$T.$$ The time required by it to travel from $$x = A$$ to $$x = \frac{A}{2}$$ is
A
$$\frac{T}{6}$$
B
$$\frac{T}{4}$$
C
$$\frac{T}{3}$$
D
$$\frac{T}{2}$$
Answer :
$$\frac{T}{6}$$
74. The bob of a simple pendulum executes simple harmonic motion in water with a period $$t,$$ while the period of oscillation of the bob is $${t_0}$$ in air. Neglecting frictional force of water and given that the density of the bob is $$\left( {\frac{4}{3}} \right) \times 1000\,kg/{m^3}.$$ What relationship between $$t$$ and $${t_0}$$ is true?
A
$$t = {t_0}$$
B
$$t = \frac{{{t_0}}}{2}$$
C
$$t = 2{t_0}$$
D
$$t = 4{t_0}$$
Answer :
$$t = 2{t_0}$$
75. The function $${\sin ^2}\left( {\omega t} \right)$$ represents
A
a periodic, but not SHM with a period $$\frac{\pi }{\omega }$$
B
a periodic, but not SHM with a period $$\frac{{2\pi }}{\omega }$$
C
a SHM with a period $$\frac{\pi }{\omega }$$
D
a SHM with a period $$\frac{{2\pi }}{\omega }$$
Answer :
a SHM with a period $$\frac{\pi }{\omega }$$
76. The particle executing simple harmonic motion has a kinetic energy $${K_0}{\cos ^2}\omega t.$$ The maximum values of the potential energy and the total energy are respectively
A
$$0\,\,{\text{and}}\,\,2{K_0}$$
B
$$\frac{{{K_0}}}{2}\,\,{\text{and}}\,\,{K_0}$$
C
$${K_0}\,\,{\text{and}}\,\,2{K_0}$$
D
$${K_0}\,\,{\text{and}}\,\,{K_0}$$
Answer :
$${K_0}\,\,{\text{and}}\,\,{K_0}$$
77. In case of a forced vibration, the resonance wave becomes very sharp when the
A
quality factor is small
B
damping force is small
C
restoring force is small
D
applied periodic force is small
Answer :
damping force is small
78. A point mass is subjected to two simultaneous sinusoidal displacements in $$x$$-direction, $${x_1}\left( t \right) = A\sin \omega t$$ and $${x_2}\left( t \right) = A\sin \left( {\omega t + \frac{{2\pi }}{3}} \right).$$ Adding a third sinusoidal displacement $${x_3}\left( t \right) = B\sin \left( {\omega t + \phi } \right)$$ brings the mass to a complete rest. The values of $$B$$ and $$\phi $$ are
A
$$\sqrt 2 A,\frac{{3p}}{4}$$
B
$$A,\frac{{4p}}{3}$$
C
$$\sqrt 3 A,\frac{{5p}}{6}$$
D
$$A,\frac{p}{3}$$
Answer :
$$A,\frac{{4p}}{3}$$
79. The angular velocity and the amplitude of a simple pendulum is $$\omega $$ and $$a$$ respectively. At a displacement $$x$$ from the mean position, if its kinetic energy is $$T$$ and potential energy is $$U,$$ then the ratio of $$T$$ to $$U$$ is
A
$$\left( {\frac{{{a^2} - {x^2}{\omega ^2}}}{{{x^2}{\omega ^2}}}} \right)$$
B
$$\frac{{{x^2}{\omega ^2}}}{{\left( {{a^2} - {x^2}{\omega ^2}} \right)}}$$
C
$$\frac{{\left( {{a^2} - {x^2}} \right)}}{{{x^2}}}$$
D
$$\frac{{{x^2}}}{{\left( {{a^2} - {x^2}} \right)}}$$
Answer :
$$\frac{{\left( {{a^2} - {x^2}} \right)}}{{{x^2}}}$$
80.
The $$x-t$$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $$t = \frac{4}{3}s$$ is

A
$$\frac{{\sqrt 3 }}{{32}}{\pi ^2}cm/{s^2}$$
B
$$\frac{{ - {\pi ^2}}}{{32}}cm/{s^2}$$
C
$$\frac{{{\pi ^2}}}{{32}}cm/{s^2}$$
D
$$ - \frac{{\sqrt 3 }}{{32}}{\pi ^2}cm/{s^2}$$
Answer :
$$ - \frac{{\sqrt 3 }}{{32}}{\pi ^2}cm/{s^2}$$