61. If $$x,v$$ and $$a$$ denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period $$T,$$ then, which of the following does not change with time?
A
$$\frac{{aT}}{x}$$
B
$$aT + 2\pi v$$
C
$$\frac{{aT}}{v}$$
D
$${a^2}{T^2} + 4{\pi ^2}{v^2}$$
Answer :
$$\frac{{aT}}{x}$$
62. The time period of a simple pendulum is $$2\,s.$$ If its length is increased by 4 times, then its period becomes
A
$$16\,s.$$
B
$$12\,s.$$
C
$$8\,s.$$
D
$$4\,s.$$
Answer :
$$4\,s.$$
63.
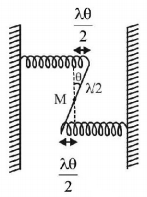
A uniform rod of length $$L$$ and mass $$M$$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $$k.$$ The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $$\theta $$ in one direction and released. The frequency of oscillation is

A
$$\frac{1}{{2\pi }}\sqrt {\frac{{2k}}{M}} $$
B
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{M}} $$
C
$$\frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} $$
D
$$\frac{1}{{2\pi }}\sqrt {\frac{{24k}}{M}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{6k}}{M}} $$
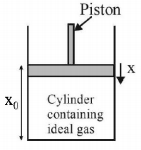
64. An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $$M.$$ The piston and the cylinder have equal cross sectional area $$A.$$ When the piston is in equilibrium, the volume of the gas is $${V_0}$$ and its pressure is $${P_0.}$$ The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
A
$$\frac{1}{{2\pi }}\frac{{A\gamma {P_0}}}{{{V_0}M}}$$
B
$$\frac{1}{{2\pi }}\frac{{{V_0}M{P_0}}}{{{A^2}\gamma }}$$
C
$$\frac{1}{{2\pi }}\sqrt {\frac{{{A^2}\gamma {P_0}}}{{MV}}} $$
D
$$\frac{1}{{2\pi }}\sqrt {\frac{{M{V_0}}}{{A\gamma {P_0}}}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{{A^2}\gamma {P_0}}}{{MV}}} $$
65. A particle at the end of a spring executes S.H.M with a period $${t_1}.$$ while the corresponding period for another spring is $${t_2}.$$ If the period of oscillation with the two springs in series is $$T$$ then
A
$${T^{ - 1}} = t_1^{ - 1} + t_2^{ - 1}$$
B
$${T^2} = t_1^2 + t_2^2$$
C
$$T = {t_1} + {t_2}$$
D
$${T^{ - 2}} = t_1^{ - 2} + t_2^{ - 2}$$
Answer :
$${T^2} = t_1^2 + t_2^2$$
66. Masses $${M_A}$$ and $${M_B}$$ hanging from the ends of strings of lengths $${L_A}$$ and $${L_B}$$ are executing simple harmonic motions. If their frequencies are $${f_A} = 2{f_B},$$ then
A
$${L_A} = 2{L_B}\,{\text{and}}\,{M_A} = \frac{{{M_B}}}{2}$$
B
$${L_A} = 4{L_B}$$ regardless of masses
C
$${L_A} = \frac{{{L_B}}}{4}$$ regardless of masses
D
$${L_A} = 2{L_B}\,{\text{and}}\,{M_A} = 2{M_B}$$
Answer :
$${L_A} = \frac{{{L_B}}}{4}$$ regardless of masses
67. A particle executing simple harmonic motion of amplitude $$5\,cm$$ has maximum speed of $$31.4\,cm/s.$$ The frequency of its oscillation is
A
$$3\,Hz$$
B
$$2\,Hz$$
C
$$4\,Hz$$
D
$$1\,Hz$$
Answer :
$$1\,Hz$$
68. A particle of mass $$m$$ executes simple harmonic motion with amplitude $$a$$ and frequency $$v.$$ The average kinetic energy during its motion from the position of equilibrium to the end is
A
$$2{\pi ^2}m{a^2}{v^2}$$
B
$${\pi ^2}m{a^2}{v^2}$$
C
$$\frac{1}{4}m{a^2}{v^2}$$
D
$$4{\pi ^2}m{a^2}{v^2}$$
Answer :
$${\pi ^2}m{a^2}{v^2}$$
69. A particle of mass $$m$$ executes simple harmonic motion with amplitude $$a$$ and frequency $$\nu .$$The average kinetic energy during its motion from the position of equilibrium to the end is
A
$$2{\pi ^2}m{a^2}{\nu ^2}$$
B
$${\pi ^2}m{a^2}{\nu ^2}$$
C
$$\frac{1}{4}m{a^2}{\nu ^2}$$
D
$$4{\pi ^2}m{a^2}{\nu ^2}$$
Answer :
$${\pi ^2}m{a^2}{\nu ^2}$$
70. Two particles are executing simple harmonic motion of the same amplitude $$A$$ and frequency $$\omega $$ along the $$x$$-axis. Their mean position is separated by distance $${X_0}\left( {{X_0} > A} \right).$$ If the maximum separation between them is $$\left( {{X_0} + A} \right),$$ the phase difference between their motion is:
A
$$\frac{\pi }{3}$$
B
$$\frac{\pi }{4}$$
C
$$\frac{\pi }{6}$$
D
$$\frac{\pi }{2}$$
Answer :
$$\frac{\pi }{2}$$