51. A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of $${10^{12}}/\sec .$$ What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avagadro number = $$6.02 \times {10^{23}}gm\,mol{e^{ - 1}}$$ )
A
$$6.4 N/m$$
B
$$7.1 N/m$$
C
$$2.2 N/m$$
D
$$5.5 N/m$$
Answer :
$$7.1 N/m$$
52. A simple harmonic oscillator has an amplitude $$a$$ and time period $$T.$$ The time required by it to travel from $$x = a$$ to $$x = \frac{a}{2}$$ is
A
$$\frac{T}{6}$$
B
$$\frac{T}{4}$$
C
$$\frac{T}{3}$$
D
$$\frac{T}{2}$$
Answer :
$$\frac{T}{6}$$
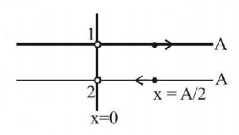
53. Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes, They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is
A
0
B
$$\frac{{2\pi }}{3}$$
C
$$\pi $$
D
$$\frac{{\pi }}{6}$$
Answer :
$$\frac{{2\pi }}{3}$$
54.
A particle starts with $$S.H.M.$$ from the mean position as shown in figure below. Its amplitude is $$A$$ and its time period is $$T.$$ At one time, its speed is half that of the maximum speed. What is the displacement at that time ?
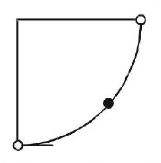
A
$$\frac{{\sqrt 2 A}}{3}$$
B
$$\frac{{\sqrt 3 A}}{2}$$
C
$$\frac{{2A}}{{\sqrt 3 }}$$
D
$$\frac{{3A}}{{\sqrt 2 }}$$
Answer :
$$\frac{{\sqrt 3 A}}{2}$$
55. If a simple pendulum has significant amplitude (upto a factor of $$\frac{1}{e}$$ of original) only in the period between $$t = 0s$$ to $$t = \tau s,$$ then $$\tau $$ may be called the average life of the pendulum. when the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with $$b$$ as the constant of proportionality, the average life time of the pendulum is (assuming damping the small) in seconds
A
$$\frac{{0.693}}{b}$$
B
$$b$$
C
$$\frac{1}{b}$$
D
$$\frac{2}{b}$$
Answer :
$$\frac{2}{b}$$
56. A particle of mass $$10\,gm$$ is describing $$S.H.M.$$ along a straight line with period of $$2\,\sec$$ and amplitude of $$10\,cm.$$ Its kinetic energy when it is at $$5\,cm$$ from its equilibrium position is
A
$$37.5\,{\pi ^2}ergs$$
B
$$3.75\,{\pi ^2}ergs$$
C
$$375\,{\pi ^2}ergs$$
D
$$0.375\,{\pi ^2}ergs$$
Answer :
$$375\,{\pi ^2}ergs$$
57. A string is stretched between fixed points separated by $$75.0\,cm.$$ It is observed to have resonant frequencies of $$420\,Hz$$ and $$315\,Hz.$$ There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
A
$$155\,Hz$$
B
$$205\,Hz$$
C
$$10.5\,Hz$$
D
$$105\,Hz$$
Answer :
$$105\,Hz$$
58. A point performs simple harmonic oscillation of period $$T$$ and the equation of motion is given by $$x = a\sin \left( {\omega t + \frac{\pi }{6}} \right).$$ After the elapse of what fraction of the time period, the velocity of the point will be equal to half of its maximum velocity ?
A
$$\frac{T}{8}$$
B
$$\frac{T}{6}$$
C
$$\frac{T}{3}$$
D
$$\frac{T}{12}$$
Answer :
$$\frac{T}{12}$$
59.
A block of mass $$m,$$ lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant $$k.$$ The other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force $$F,$$ the maximum speed of the block is:
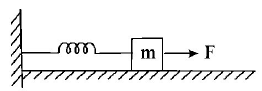
A
$$\frac{{2F}}{{\sqrt {mk} }}$$
B
$$\frac{F}{{\pi \sqrt {mk} }}$$
C
$$\frac{{\pi F}}{{\sqrt {mk} }}$$
D
$$\frac{F}{{\sqrt {mk} }}$$
Answer :
$$\frac{F}{{\sqrt {mk} }}$$
60. The average value of potential energy for one complete oscillation cycle of a body of mass $$m$$ executing $$S.H.M.$$ having angular frequency $$\omega $$ and maximum amplitude $$a$$ is given by :
A
$$\frac{1}{2}m{\omega ^2}{a^2}$$
B
$$\frac{1}{4}m{\omega ^2}{a^2}$$
C
$$\frac{1}{8}m{\omega ^2}{a^2}$$
D
$$\frac{1}{{16}}m{\omega ^2}{a^2}$$
Answer :
$$\frac{1}{4}m{\omega ^2}{a^2}$$