41. The bob of a simple pendulum executes simple harmonic motion in water with a period $$t,$$ while the period of oscillation of the bob is $${t_0}$$ in air. Neglecting frictional force of water and given that the density of the bob is $$\left( {\frac{4}{3}} \right) \times 1000kg/{m^3}.$$ What relationship between $$t$$ and $${t_0}$$ is true
A
$$t = 2{t_0}$$
B
$$t = \frac{{{t_0}}}{2}$$
C
$$t = {t_0}$$
D
$$t = 4{t_0}$$
Answer :
$$t = 2{t_0}$$
42. In forced oscillation of a particle the amplitude is maximum for a frequency $${\omega _1}$$ of the force while the energy is maximum for a frequency $${\omega _2}$$ of the force; then
A
$${\omega _1} < {\omega _2}$$ when damping is small and $${\omega _1} > {\omega _2}$$ when damping is large
B
$${\omega _1} > {\omega _2}$$
C
$${\omega _1} = {\omega _2}$$
D
$${\omega _1} < {\omega _2}$$
Answer :
$${\omega _1} = {\omega _2}$$
43. A body executes $$SHM$$ with an amplitude $$a.$$ At what displacement from the mean position, the potential energy of the body is one-fourth of its total energy ?
A
$$\frac{a}{4}$$
B
$$\frac{a}{2}$$
C
$$\frac{3a}{4}$$
D
Some other fraction of $$a$$
Answer :
$$\frac{a}{2}$$
44. If a simple harmonic motion is represented by $$\frac{{{d^2}x}}{{d{t^2}}} + \alpha x = 0,$$ its time period is
A
$$\frac{{2\pi }}{{\sqrt \alpha }}$$
B
$$\frac{{2\pi }}{\alpha }$$
C
$$2\pi \sqrt \alpha $$
D
$$2\pi \alpha $$
Answer :
$$\frac{{2\pi }}{{\sqrt \alpha }}$$
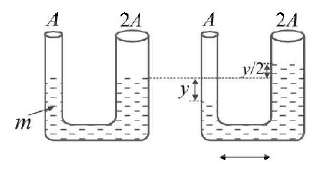
45.
A $$U$$-tube is of non uniform cross-section. The area of cross-sections of two sides of tube are $$A$$ and $$2A$$ (see fig.). It contains non-viscous liquid of mass $$m.$$ The liquid is displaced slightly and free to oscillate. Its time period of oscillations is

A
$$T = 2\pi \sqrt {\frac{m}{{3\rho gA}}} $$
B
$$T = 2\pi \sqrt {\frac{m}{{2\rho gA}}} $$
C
$$T = 2\pi \sqrt {\frac{m}{{\rho gA}}} $$
D
None of these
Answer :
$$T = 2\pi \sqrt {\frac{m}{{3\rho gA}}} $$
46. The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are
A
$$kg\,m{s^{ - 1}}$$
B
$$kg\,m{s^{ - 2}}$$
C
$$kg\,{s^{ - 1}}$$
D
$$kg\,s$$
Answer :
$$kg\,{s^{ - 1}}$$
47. A simple pendulum oscillating in air has period $$T.$$ The bob of the pendulum is completely immersed in a non-viscous liquid. The density of the liquid is $$\frac{1}{{16}}$$ th of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is :
A
$$2T\sqrt {\frac{l}{{10}}} $$
B
$$2T\sqrt {\frac{l}{{14}}} $$
C
$$4T\sqrt {\frac{l}{{15}}} $$
D
$$4T\sqrt {\frac{l}{{14}}} $$
Answer :
$$4T\sqrt {\frac{l}{{15}}} $$
48. A particle moves with simple harmonic motion in a straight line. In first $$\tau s,$$ after starting from rest it travels a distance $$a,$$ and in next $$\tau s$$ it travels $$2a,$$ in same direction, then:
A
amplitude of motion is $$3a$$
B
time period of oscillations is 8$$\tau $$
C
amplitude of motion is $$4a$$
D
time period of oscillations is 6$$\tau $$
Answer :
time period of oscillations is 6$$\tau $$
49. In a simple harmonic oscillator, at the mean position
A
kinetic energy is minimum, potential energy is maximum
B
both kinetic and potential energies are maximum
C
kinetic energy is maximum, potential energy is minimum
D
both kinetic and potential energies are minimum.
Answer :
kinetic energy is maximum, potential energy is minimum
50.
Two springs, each of spring constant $$k = 100\,N/m,$$ are attached to a block of mass $$2\,kg$$ as shown in the figure. The block can slide smoothly along a horizontal platform clamped to the opposite walls of the trolley of mass $$5\,kg.$$ If the block is displaced by $$x\,cm.$$ and released, the period of oscillation in seconds is

A
$$T = 2\pi \sqrt {\frac{1}{{20}}} $$
B
$$T = 2\pi \sqrt {\frac{7}{{1000}}} $$
C
$$T = 2\pi \sqrt {\frac{1}{{140}}} $$
D
$$T = 2\pi \frac{{49}}{{100}}$$
Answer :
$$T = 2\pi \sqrt {\frac{1}{{140}}} $$