31.
What do you conclude from the graph about the frequency of $$KE, PE$$ and $$SHM$$ ?

A
Frequency of $$KE$$ and $$PE$$ is double the frequency of $$SHM.$$
B
Frequency of $$KE$$ and $$PE$$ is four times the frequency $$SHM.$$
C
Frequency of $$PE$$ is double the frequency of $$KE.$$
D
Frequency of $$KE$$ and $$PE$$ is equal to the frequency of $$SHM.$$
Answer :
Frequency of $$KE$$ and $$PE$$ is double the frequency of $$SHM.$$
32.
The potential energy of a simple harmonic oscillator when the particle is half way to its end point is
(where, $$E$$ is the total energy)
A
$$\frac{1}{4}E$$
B
$$\frac{1}{2}E$$
C
$$\frac{2}{3}E$$
D
$$\frac{1}{8}E$$
Answer :
$$\frac{1}{4}E$$
33.
The displacement vs time of a particle executing $$SHM$$ is shown in figure.
The initial phase $$\phi $$ is
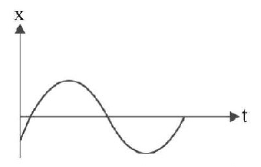
A
$$ - \pi < \phi < - \frac{\pi }{2}$$
B
$$\pi < \phi < \frac{{3\pi }}{2}$$
C
$$ - \frac{{3\pi }}{2} < \phi < - \pi $$
D
$$\frac{\pi }{2} < \phi < \pi $$
Answer :
$$ - \pi < \phi < - \frac{\pi }{2}$$
34.
Two simple harmonic motions are represented by the equations $${y_1} = 0.1\sin \left( {100\pi t + \frac{\pi }{3}} \right)$$ and $${y_2} = 0.1\cos \pi t.$$
The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is
A
$${\frac{\pi }{3}}$$
B
$$\frac{{ - \pi }}{6}$$
C
$${\frac{\pi }{6}}$$
D
$$\frac{{ - \pi }}{3}$$
Answer :
$$\frac{{ - \pi }}{6}$$
35. A particle of mass $$1\,kg$$ is placed in a potential field. Its potential energy is given by $$U = 10{x^2} + 5.$$ The frequency of oscillations of the particle is given by
A
$$\left( {\sqrt {10} } \right)$$
B
$$\left( {\sqrt {5} } \right)$$
C
$$\left( {\sqrt {\frac{{10}}{\pi }} } \right)$$
D
$$\left( {\frac{{\sqrt 5 }}{\pi }} \right)$$
Answer :
$$\left( {\frac{{\sqrt 5 }}{\pi }} \right)$$
36. In $$SHM$$ restoring force is $$F = - kx,$$ where $$k$$ is force constant, $$x$$ is displacement and $$a$$ is amplitude of motion, then total energy depends upon
A
$$k,a$$ and $$m$$
B
$$k, x, m$$
C
$$k, a$$
D
$$k, x$$
Answer :
$$k, a$$
37. A particle executes simple harmonic oscillation with an amplitude $$a.$$ The period of oscillation is $$T.$$ The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
A
$$\frac{T}{4}$$
B
$$\frac{T}{8}$$
C
$$\frac{T}{12}$$
D
$$\frac{T}{2}$$
Answer :
$$\frac{T}{12}$$
38. Two simple harmonic motions of angular frequency $$100\,rad\,{s^{ - 1}}$$ and $$1000\,rad\,{s^{ - 1}}$$ have the same displacement amplitude. The ratio of their maximum accelerations is
A
$$1:10$$
B
$$1:{10^2}$$
C
$$1:{10^3}$$
D
$$1:{10^4}$$
Answer :
$$1:{10^2}$$
39. The displacement of an object attached to a spring and executing simple harmonic motion is given by $$x = 2 \times {10^{ - 2}}\cos \pi t$$ metre. The time at which the maximum speed first occurs is
A
$$0.25 s$$
B
$$0.5 s$$
C
$$0.75 s$$
D
$$0.125 s$$
Answer :
$$0.5 s$$
40.
For a particle executing SHM the displacement $$x$$ is given by $$x = A\cos \omega t.$$ Identify the graph which represents the variation of potential energy $$\left( {PE} \right)$$ as a function of time $$t$$ and displacement $$x$$

A
I, III
B
II, IV
C
II, III
D
I, IV
Answer :
I, III