21. When the displacement of a particle executing simple harmonic motion is half of its amplitude, the ratio of its kinetic energy to potential energy is
A
$$1 : 3$$
B
$$2 : 1$$
C
$$3 : 1$$
D
$$1 : 2$$
Answer :
$$3 : 1$$
22.
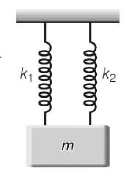
A mass is suspended separately by two springs of spring constants $${k_1}$$ and $${k_2}$$ in successive order. The time periods of oscillations in the two cases are $${T_1}$$ and $${T_2}$$ respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is $$T.$$ The correct relation is
A
$${T^2} = T_1^2 + T_2^2$$
B
$${T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2}$$
C
$${T^{ - 1}} = T_1^{ - 1} + T_2^{ - 1}$$
D
$$T = {T_1} + {T_2}$$
Answer :
$${T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2}$$
23.
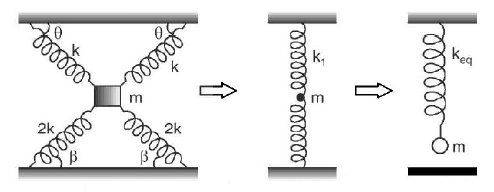
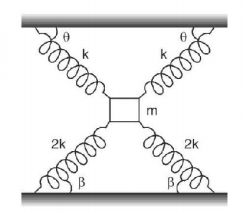
Disregarding gravity, find the period of oscillation of the particle connected with four springs as shown in the figure.
(Given : $$\theta = {45^ \circ },\beta = {30^ \circ }$$ )
A
$$\pi \sqrt {\frac{{2m}}{k}} $$
B
$$\sqrt {\frac{{2m\pi }}{k}} $$
C
$$\sqrt {\frac{{m\pi }}{{2k}}} $$
D
$$\pi \sqrt {\frac{m}{{2k}}} $$
Answer :
$$\pi \sqrt {\frac{{2m}}{k}} $$
24. A particle starts simple harmonic motion from the mean position. Its amplitude is a and time period is $$T.$$ What is its displacement when its speed is half of its maximum speed ?
A
$$\frac{{\sqrt 2 }}{3}a$$
B
$$\frac{{\sqrt 3 }}{2}a$$
C
$$\frac{2}{{\sqrt 3 }}a$$
D
$$\frac{a}{{\sqrt 2 }}$$
Answer :
$$\frac{{\sqrt 3 }}{2}a$$
25. A mass $$M$$ is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period $$T.$$ If the mass is increased by $$m,$$ the time period becomes $$\frac{{5T}}{3}.$$ Then the ratio of $$\frac{m}{M}$$ is
A
$$\frac{3}{5}$$
B
$$\frac{{25}}{9}$$
C
$$\frac{{16}}{9}$$
D
$$\frac{5}{3}$$
Answer :
$$\frac{{16}}{9}$$
26. A particle is executing simple harmonic motion with amplitude $$A.$$ When the ratio of its kinetic energy to the potential energy is $$\frac{1}{4},$$ its displacement from its mean position is
A
$$\frac{2}{{\sqrt 5 }}A$$
B
$$\frac{{\sqrt 3 }}{2}A$$
C
$$\frac{3}{4}A$$
D
$$\frac{1}{4}A$$
Answer :
$$\frac{2}{{\sqrt 5 }}A$$
27. A body executes simple harmonic motion. The potential energy $$\left( {P.E} \right),$$ the kinetic energy $$\left( {K.E} \right)$$ and total energy $$\left( {T.E} \right)$$ are measured as a function of displacement $$x.$$ Which of the following statements is true?
A
$$K.E.$$ is maximum when $$x = 0$$
B
$$T.E.$$ is zero when $$x = 0$$
C
$$K.E.$$ is maximum when $$x$$ is maximum
D
$$P.E.$$ is maximum when $$x = 0$$
Answer :
$$K.E.$$ is maximum when $$x = 0$$
28.
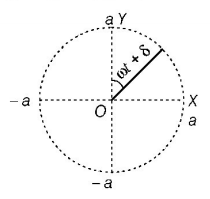
Two simple harmonic motions given by,
$$x = a\sin \left( {\omega t + \delta } \right)$$ and $$y = a\sin $$
$$\left( {\omega t + \delta + \frac{\pi }{2}} \right)$$ act on a particle simultaneously, then the motion of particle will be
A
circular anti-clockwise
B
circular clockwise
C
elliptical anti-clockwise
D
elliptical clockwise
Answer :
circular clockwise
29. A particle is executing simple harmonic motion with a time period $$T.$$ At time $$t = 0,$$ it is at its position of equilibrium. The kinetic energy-time graph of the particle will look like:
A


B


C


D


Answer :


30. A particle executes simple harmonic motion between $$x = - A$$ and $$x = + A.$$ The time taken for it to go from 0 to $$\frac{A}{2}$$ is $${T_1}$$ and to go from $$\frac{A}{2}$$ to $$A$$ is $${T_2.}$$ Then
A
$${T_1} < {T_2}$$
B
$${T_1} > {T_2}$$
C
$${T_1} = {T_2}$$
D
$${T_1} = 2{T_2}$$
Answer :
$${T_1} < {T_2}$$