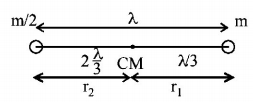
11. A body is executing simple harmonic motion. At a displacement $$x$$ from mean position, its potential energy is $${E_1} = 2J$$ and at a displacement $$y$$ from mean position, its potential energy is $${E_2} = 8J.$$ The potential energy $$E$$ at a displacement $$\left( {x + y} \right)$$ from mean position is
A
$$10J$$
B
$$14J$$
C
$$18J$$
D
$$4J$$
Answer :
$$18J$$
12. If a simple harmonic oscillator has got a displacement of $$0.02\,m$$ and acceleration equal to $$2.0\,m/{s^2}$$ at any time, the angular frequency of the oscillator is equal to
A
$$10\,rad/s$$
B
$$0.1\,rad/s$$
C
$$100\,rad/s$$
D
$$1\,rad/s$$
Answer :
$$10\,rad/s$$
13. A mass $$m$$ is vertically suspended from a spring of negligible mass, the system oscillates with a frequency $$n.$$ What will be the frequency of the system, if a mass $$4m$$ is suspended from the same spring ?
A
$$\frac{n}{4}$$
B
$$4\,n$$
C
$$\frac{n}{2}$$
D
$$2\,n$$
Answer :
$$\frac{n}{2}$$
14. Two bodies $$M$$ and $$N$$ of equal masses are suspended from two separate massless springs of spring constants $${k_1}$$ and $${k_2}$$ respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of $$M$$ to that of $$N$$ is
A
$$\frac{{{k_1}}}{{{k_2}}}$$
B
$$\sqrt {\frac{{{k_1}}}{{{k_2}}}} $$
C
$$\frac{{{k_2}}}{{{k_1}}}$$
D
$$\sqrt {\frac{{{k_2}}}{{{k_1}}}} $$
Answer :
$$\sqrt {\frac{{{k_2}}}{{{k_1}}}} $$
15.
A small block is connected to one end of a massless spring of un-stretched length $$4.9m.$$ The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by $$0.2m$$ and released from rest at $$t = 0.$$ It then executes simple harmonic motion with angular frequency $$\omega = \frac{\pi }{3}rad/s.$$ Simultaneously at $$t = 0,$$ a small pebble is projected with speed $$v$$ form point $$P$$ at an angle of $${45^ \circ }$$ as shown in the figure. Point $$P$$ is at a horizontal distance of $$10m$$ from $$O.$$ If the pebble hits the block at $$t = 1s,$$ the value of $$v$$ is (take $$g = 10m/{s^2}$$ )

A
$$\sqrt {50} m/s$$
B
$$\sqrt {51} m/s$$
C
$$\sqrt {52} m/s$$
D
$$\sqrt {53} m/s$$
Answer :
$$\sqrt {50} m/s$$
16. A point mass oscillates along the $$x$$-axis according to the law $$x = {x_0}\cos \left( {\omega t - \frac{\pi }{4}} \right).$$ If the acceleration of the particle is written as $$a = A\cos \left( {\omega t + \delta } \right),$$ then
A
$$A = {x_0}{\omega ^2},\delta = \frac{{3\pi }}{4}$$
B
$$A = {x_0},\delta = \frac{{ - \pi }}{4}$$
C
$$A = {x_0}{\omega ^2},\delta = \frac{\pi }{4}$$
D
$$A = {x_0}{\omega ^2},\delta = \frac{{ - \pi }}{4}$$
Answer :
$$A = {x_0}{\omega ^2},\delta = \frac{{3\pi }}{4}$$
17. Two simple pendulums of length $$0.5\,m$$ and $$2.0\,m$$ respectively are given small linear displacement in one direction at the same time. They will again be in the same phase when the pendulum of shorter length has completed oscillations
A
5
B
1
C
2
D
3
Answer :
2
18.
Two masses $$m$$ and $$\frac{m}{2}$$ are connected at the two ends of a massless rigid rod of length $$l.$$ The rod is suspended by a thin wire of torsional constant $$k$$ at the centre of mass of the rod-mass system (see figure). Because of torsional constant $$k,$$ the restoring toruque is $$\tau = k\theta $$ for angular displacement $$\theta .$$ If the rod is rotated by $${\theta _0}$$ and released, the tension in it when it passes through its mean position will be:
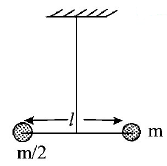
A
$$\frac{{3k{\theta _0}^2}}{l}$$
B
$$\frac{{2k{\theta _0}^2}}{l}$$
C
$$\frac{{k{\theta _0}^2}}{l}$$
D
$$\frac{{k{\theta _0}^2}}{{2l}}$$
Answer :
$$\frac{{k{\theta _0}^2}}{l}$$
19. The angular velocity and the amplitude of a simple pendulum is $$\omega $$ and $$a$$ respectively. At a displacement $$x$$ from the mean position if its kinetic energy is $$T$$ and potential energy is $$V,$$ then the ratio of $$T$$ to $$V$$ is
A
$$\frac{{\left( {{a^2} - {x^2}{\omega ^2}} \right)}}{{{x^2}{\omega ^2}}}$$
B
$$\frac{{{x^2}{\omega ^2}}}{{\left( {{a^2} - {x^2}{\omega ^2}} \right)}}$$
C
$$\frac{{\left( {{a^2} - {x^2}} \right)}}{{{x^2}}}$$
D
$$\frac{{{x^2}}}{{\left( {{a^2} - {x^2}} \right)}}$$
Answer :
$$\frac{{\left( {{a^2} - {x^2}} \right)}}{{{x^2}}}$$
20.
A rod of mass $$M$$ and length $$L$$ is hinged at its centre of mass so that it can rotate in a vertical plane. Two springs each of stiffness $$k$$ are connected at its ends, as shown in the figure. The time period of $$SHM$$ is
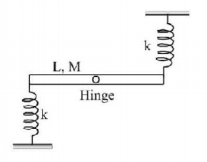
A
$$2\,\pi \sqrt {\frac{M}{{6k}}} $$
B
$$2\,\pi \sqrt {\frac{M}{{3k}}} $$
C
$$2\,\pi \sqrt {\frac{{ML}}{k}} $$
D
$$\pi \sqrt {\frac{M}{{6k}}} $$
Answer :
$$2\,\pi \sqrt {\frac{M}{{6k}}} $$