171. A particle of mass $$1\,kg$$ is moving in $$S.H.M.$$ with an amplitude 0.02 and a frequency of $$60\,Hz.$$ The maximum force acting on the particle is
A
$$144\,{\pi ^2}$$
B
$$188\,{\pi ^2}$$
C
$$288\,{\pi ^2}$$
D
None of these
Answer :
$$288\,{\pi ^2}$$
172. Two springs of spring constants $${k_1}$$ and $${k_2}$$ are joined in series. The effective spring constant of the combination is given by
A
$$\sqrt {{k_1}{k_2}} $$
B
$$\frac{{\left( {{k_1} + {k_2}} \right)}}{2}$$
C
$${k_1} + {k_2}$$
D
$$\frac{{{k_1}{k_2}}}{{\left( {{k_1} + {k_2}} \right)}}$$
Answer :
$$\frac{{{k_1}{k_2}}}{{\left( {{k_1} + {k_2}} \right)}}$$
173. Starting from the origin a body oscillates simple harmonically with a period of $$2s.$$ After what time will its kinetic energy be 75% of the total energy?
A
$$\frac{1}{6}s$$
B
$$\frac{1}{4}s$$
C
$$\frac{1}{3}s$$
D
$$\frac{1}{{12}}s$$
Answer :
$$\frac{1}{6}s$$
174. Two simple harmonic motions are represented by the equations $${y_1} = 0.1\sin \left( {100\pi t + \frac{\pi }{3}} \right)$$ and $${y_2} = 0.1\cos \pi t.$$ The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is
A
$$\frac{\pi }{3}$$
B
$$\frac{{ - \pi }}{6}$$
C
$$\frac{\pi }{6}$$
D
$$\frac{{ - \pi }}{3}$$
Answer :
$$\frac{{ - \pi }}{6}$$
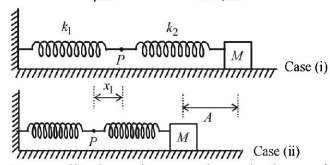
175.
The mass $$M$$ shown in the figure oscillates in simple harmonic motion with amplitude $$A.$$ The amplitude of the point $$P$$ is
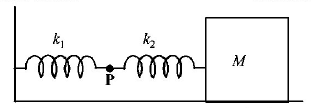
A
$$\frac{{{k_1}A}}{{{k_2}}}$$
B
$$\frac{{{k_2}A}}{{{k_1}}}$$
C
$$\frac{{{k_1}A}}{{{k_1} + {k_2}}}$$
D
$$\frac{{{k_2}A}}{{{k_1} + {k_2}}}$$
Answer :
$$\frac{{{k_2}A}}{{{k_1} + {k_2}}}$$
176. A particle executing harmonic motion is having velocities $${v_1}$$ and $${v_2}$$ at distances is $${x_1}$$ and $${x_2}$$ from the equilibrium position. The amplitude of the motion is
A
$$\sqrt {\frac{{v_1^2{x_2} - v_2^2{x_1}}}{{v_1^2 + v_2^2}}} $$
B
$$\sqrt {\frac{{v_1^2x_1^2 - v_2^2x_2^2}}{{v_1^2 + v_2^2}}} $$
C
$$\sqrt {\frac{{v_1^2x_2^2 - v_2^2x_1^2}}{{v_1^2 - v_2^2}}} $$
D
$$\sqrt {\frac{{v_1^2x_2^2 + v_2^2x_1^2}}{{v_1^2 + v_2^2}}} $$
Answer :
$$\sqrt {\frac{{v_1^2x_2^2 - v_2^2x_1^2}}{{v_1^2 - v_2^2}}} $$