141. The composition of two simple harmonic motions of equal periods at right angle to each other and with a phase difference of $$\pi $$ results in the displacement of the particle along
A
circle
B
figure of eight
C
straight line
D
ellipse
Answer :
straight line
142. A mass $$M,$$ attached to a horizontal spring, executes S.H.M. with amplitude $${A_1.}$$ When the mass $$M$$ passes through its mean position then a smaller mass $$m$$ is placed over it and both of them move together with amplitude $${A_2.}$$ The ratio of $$\left( {\frac{{{A_1}}}{{{A_2}}}} \right)$$ is
A
$$\frac{{M + m}}{M}$$
B
$${\left( {\frac{M}{{M + m}}} \right)^{\frac{1}{2}}}$$
C
$${\left( {\frac{{M + m}}{M}} \right)^{\frac{1}{2}}}$$
D
$$\frac{M}{{M + m}}$$
Answer :
$${\left( {\frac{{M + m}}{M}} \right)^{\frac{1}{2}}}$$
143. Which one of the following statements is true for the speed $$v$$ and the acceleration $$\alpha $$ of a particle executing simple harmonic motion?
A
When $$v$$ is maximum, $$\alpha $$ is maximum
B
Value of $$\alpha $$ is zero, whatever may be the value of $$v$$
C
When $$v$$ is zero, $$\alpha $$ is Zero
D
When $$v$$ is maximum, $$\alpha $$ is zero
Answer :
When $$v$$ is maximum, $$\alpha $$ is zero
144. A particle at the end of a spring executes $$S.H.M$$ with a period $${t_1},$$ while the corresponding period for another spring is $${t_2}.$$ If the period of oscillation with the two springs in series is $$T$$ then
A
$${T^{ - 1}} = t_1^{ - 1} + t_2^{ - 1}$$
B
$${T^2} = t_1^2 + t_2^2$$
C
$$T = {t_1} + {t_2}$$
D
$${T^{ - 2}} = t_1^{ - 2} + t_2^{ - 2}$$
Answer :
$${T^2} = t_1^2 + t_2^2$$
145. A body is executing $$SHM.$$ When the displacements from the mean position is $$4\,cm$$ and $$5\,cm,$$ the corresponding velocities of the body is $$10\,cm/s$$ and $$8\,cm/s.$$ Then, the time period of the body is
A
$$2\,\pi \sec $$
B
$$\frac{\pi }{2}\sec $$
C
$$\pi \sec $$
D
$$\frac{3\pi }{2}\sec $$
Answer :
$$\pi \sec $$
146. A second’s pendulum is placed in a space laboratory orbiting around the earth at a height $$3\,R$$ from the earth’s surface where $$R$$ is earth’s radius. The time period of the pendulum will be
A
zero
B
$$2\sqrt 3 $$
C
$$4\,\sec$$
D
infinite
Answer :
infinite
147. The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is $$10\,{s^{ - 1}}.$$ At, $$t = 0$$ the displacement is $$5\,m.$$ The initial phase is $$\frac{\pi }{4}.$$ What is the maximum acceleration ?
A
$$500\,m/{s^2}$$
B
$$500\sqrt 2 \,m/{s^2}$$
C
$$750\,m/{s^2}$$
D
$$750\sqrt 2 \,m/{s^2}$$
Answer :
$$500\sqrt 2 \,m/{s^2}$$
148. A particle of mass $$m$$ oscillates with simple harmonic motion between points $${x_1}$$ and $${x_2},$$ the equilibrium position being $$O.$$ Its potential energy is plotted. It will be as given below in the graph.
A


B


C


D


Answer :


149. A simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration $$\alpha ,$$ then the time period is given by $$T = 2\pi \sqrt {\left( {\frac{l}{g}} \right)} ,$$ where $$g$$ is equal to
A
$$g$$
B
$$g - \alpha $$
C
$$g + \alpha $$
D
$$\sqrt {\left( {{g^2} + {\alpha ^2}} \right)} $$
Answer :
$$\sqrt {\left( {{g^2} + {\alpha ^2}} \right)} $$
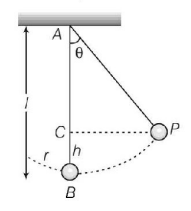
150. A pendulum is displaced to an angle $$\theta $$ from its equilibrium position, then it will pass through its mean position with a velocity $$v$$ equal to
A
$$\sqrt {2gl} $$
B
$$\sqrt {2gl\sin \theta } $$
C
$$\sqrt {2gl\cos \theta } $$
D
$$\sqrt {2gl\left( {1 - \cos \theta } \right)} $$
Answer :
$$\sqrt {2gl\left( {1 - \cos \theta } \right)} $$