131. A body is executing $$S.H.M.$$ When its displacement from the mean position are $$4\,cm$$ and $$5\,cm,$$ it has velocities $$10\,cm\,{s^{ - 1}}$$ and $$8\,cm\,{s^{ - 1}}$$ respectively. Its periodic time is
A
$$\frac{\pi }{{2s}}$$
B
$$\pi \,s$$
C
$$\frac{{3\,\pi }}{{2s}}$$
D
$$2\,\pi \,s$$
Answer :
$$\pi \,s$$
132. If a simple pendulum has significant amplitude (up to a factor of $$\frac{1}{e}$$ of original) only in the period between $$t = 0 s$$ to $$t = \tau s,$$ then $$\tau $$ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with $$b$$ as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds :
A
$$\frac{{0.693}}{b}$$
B
$$b$$
C
$$\frac{1}{b}$$
D
$$\frac{2}{b}$$
Answer :
$$\frac{2}{b}$$
133. A pendulum with time period of $$1s$$ is losing energy. At certain time its energy is $$45\,J.$$ If after completing 15 oscillations, its energy has become $$15\,J,$$ its damping constant (in $${s^{ - 1}}$$) is:
A
$$\frac{1}{2}$$
B
$$\frac{1}{{30}}\ln 3$$
C
2
D
$$\frac{1}{{15}}\ln 3$$
Answer :
$$\frac{1}{{15}}\ln 3$$
134. The maximum velocity of a particle, executing simple harmonic motion with an amplitude $$7mm,$$ is $$4.4m/s.$$ The period of oscillation is
A
$$0.001s$$
B
$$10s$$
C
$$0.1s$$
D
$$100s$$
Answer :
$$0.001s$$
135. A particle is executing a simple harmonic motion. Its maximum acceleration is $$\alpha $$ and maximum velocity is $$\beta .$$ Then, its time period of vibration will be
A
$$\frac{{{\beta ^2}}}{{{\alpha ^2}}}$$
B
$$\frac{\alpha }{\beta }$$
C
$$\frac{{{\beta ^2}}}{\alpha }$$
D
$$\frac{{2\pi \beta }}{\alpha }$$
Answer :
$$\frac{{2\pi \beta }}{\alpha }$$
136. If $$ < E > $$ and $$ < U > $$ denote the average kinetic and the average potential energies respectively of mass describing a simple harmonic motion, over one period, then the correct relation is
A
$$ < E > = < U > $$
B
$$ < E > = 2 < U > $$
C
$$ < E > = - 2 < U > $$
D
$$ < E > = - < U > $$
Answer :
$$ < E > = < U > $$
137. A particle of mass $$m$$ is attached to a spring (of spring constant $$k$$) and has a natural angular frequency $${\omega _0}.$$ An external force $$F\left( t \right)$$ proportional to $$\cos \,\omega t\left( {\omega \ne {\omega _0}} \right)$$ is applied to the oscillator. The displacement of the oscillator will be proportional to
A
$$\frac{1}{{m\left( {\omega _0^2 + {\omega ^2}} \right)}}$$
B
$$\frac{1}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}$$
C
$$\frac{m}{{\omega _0^2 - {\omega ^2}}}$$
D
$$\frac{m}{{\left( {\omega _0^2 + {\omega ^2}} \right)}}$$
Answer :
$$\frac{1}{{m\left( {\omega _0^2 - {\omega ^2}} \right)}}$$
138. The displacement of particle between maximum potential energy position and maximum kinetic energy position in simple harmonic motion is
A
$$ \pm \frac{a}{2}$$
B
$$ \pm a$$
C
$$ \pm 2a$$
D
$$ \pm 1$$
Answer :
$$ \pm a$$
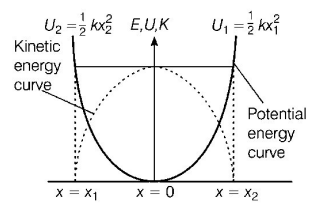
139. A particle of mass $$m$$ oscillates with simple harmonic motion between points $${x_1}$$ and $${x_2},$$ the equilibrium position being $$O.$$ Its potential energy is plotted. It will be as given below in the graph
A


B


C


D


Answer :


140.
The acceleration of a particle undergoing $$SHM$$ is graphed in figure. At point 2 the velocity of the particle is

A
zero
B
negative
C
positive
D
None of these
Answer :
zero