121. A particle executes linear simple harmonic motion with an amplitude of $$3\,cm.$$ When the particle is at $$2\,cm$$ from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
A
$$\frac{{\sqrt 5 }}{\pi }$$
B
$$\frac{{\sqrt 5 }}{{2\pi }}$$
C
$$\frac{{4\pi }}{{\sqrt 5 }}$$
D
$$\frac{{2\pi }}{{\sqrt 3 }}$$
Answer :
$$\frac{{4\pi }}{{\sqrt 5 }}$$
122. In case of sustained forced oscillations the amplitude of oscillations
A
decreases linearly
B
decreases sinusoidally
C
decreases exponentially
D
always remains constant
Answer :
decreases linearly
123. The period of oscillation of a mass $$M$$ suspended from a spring of negligible mass is $$T.$$ If along with it another mass $$M$$ is also suspended, the period of oscillation will now be
A
$$T$$
B
$$\frac{T}{{\sqrt 2 }}$$
C
$$2T$$
D
$$\sqrt 2 T$$
Answer :
$$\sqrt 2 T$$
124. A body oscillates with $$SHM$$ according to the equation (in $$SI$$ units), $$x = 5\cos \left( {2\pi t\frac{\pi }{4}} \right).$$ Its instantaneous displacement at $$t = 1\,second$$ is
A
$$\frac{{\sqrt 2 }}{5}m$$
B
$$\frac{1}{{\sqrt 3 }}m$$
C
$$\frac{5}{{\sqrt 2 }}m$$
D
$$\frac{1}{2}m$$
Answer :
$$\frac{5}{{\sqrt 2 }}m$$
125. Two particles $$A$$ and $$B$$ of equal masses are suspended from two massless springs of spring of spring constant $${k_1}$$ and $${k_2,}$$ respectively. If the maximum velocities, during oscillation, are equal, the ratio of amplitude of $$A$$ and $$B$$ is
A
$$\sqrt {\frac{{{k_1}}}{{{k_2}}}} $$
B
$$\frac{{{k_2}}}{{{k_1}}}$$
C
$$\sqrt {\frac{{{k_2}}}{{{k_1}}}} $$
D
$$\frac{{{k_1}}}{{{k_2}}}$$
Answer :
$$\sqrt {\frac{{{k_2}}}{{{k_1}}}} $$
126. A particle is executing $$SHM$$ along a straight line. Its velocities at distances $${x_1}$$ and $${x_2}$$ from the mean position are $${V_1}$$ and $${V_2},$$ respectively. Its time period is
A
$$2\pi \sqrt {\frac{{x_2^2 - x_1^2}}{{V_1^2 - V_2^2}}} $$
B
$$2\pi \sqrt {\frac{{V_1^2 + V_2^2}}{{x_1^2 + x_2^2}}} $$
C
$$2\pi \sqrt {\frac{{V_1^2 - V_2^2}}{{x_1^2 - x_2^2}}} $$
D
$$2\pi \sqrt {\frac{{x_1^2 - x_2^2}}{{V_1^2 - V_2^2}}} $$
Answer :
$$2\pi \sqrt {\frac{{x_2^2 - x_1^2}}{{V_1^2 - V_2^2}}} $$
127. In a simple harmonic motion, when the displacement is one-half the amplitude, what fraction of the total energy is kinetic?
A
Zero
B
$$\frac{1}{4}$$
C
$$\frac{1}{2}$$
D
$$\frac{3}{4}$$
Answer :
$$\frac{3}{4}$$
128. A particle of mass $$m$$ oscillates with a potential energy $$U = {U_0} + \alpha \,{x^2},$$ where $${U_0}$$ and $$\alpha $$ are constants and $$x$$ is the displacement of particle from equilibrium position. The time period of oscillation is
A
$$2\pi \sqrt {\frac{m}{\alpha }} $$
B
$$2\pi \sqrt {\frac{m}{{2\alpha }}} $$
C
$$\pi \sqrt {\frac{{2m}}{\alpha }} $$
D
$$2\pi \sqrt {\frac{m}{{{\alpha ^2}}}} $$
Answer :
$$2\pi \sqrt {\frac{m}{{2\alpha }}} $$
129.
Four massless springs whose force constants are $$2k, 2k, k$$ and $$2k$$ respectively are attached to a mass $$M$$ kept on a frictionless plane (as shown in figure). If the mass $$M$$ is displaced in the horizontal direction, then the frequency of the system is
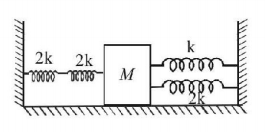
A
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{{4M}}} $$
B
$$\frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$
C
$$\frac{1}{{2\pi }}\sqrt {\frac{k}{{7M}}} $$
D
$$\frac{1}{{2\pi }}\sqrt {\frac{{7k}}{M}} $$
Answer :
$$\frac{1}{{2\pi }}\sqrt {\frac{{4k}}{M}} $$
130. Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance $$h$$ directly above the tunnel, the motion of the particle is
A
simple harmonic
B
parabolic
C
oscillatory
D
non-periodic
Answer :
oscillatory
