101. The amplitude of a particle executing $$SHM$$ is $$4\,cm.$$ At the mean position the speed of the particle is $$16\,cm/\sec.$$ The distance of the particle from the mean position at which the speed of the particle becomes $$8\sqrt 3 \,cm/s,$$ will be
A
$$2\sqrt 3 \,cm$$
B
$$\sqrt 3 \,cm$$
C
$$1\,cm$$
D
$$2\,cm$$
Answer :
$$2\,cm$$
102.
Part of a simple harmonic motion is graphed in the figure, where $$y$$ is the displacement from the mean position. The correct equation describing this $$S.H.M.$$ is
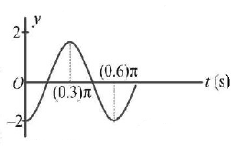
A
$$y = 4\cos \left( {0.6t} \right)$$
B
$$y = 2\sin \left( {\frac{{10}}{3}t - \frac{\pi }{2}} \right)$$
C
$$y = 4\sin \left( {\frac{{10}}{3}t + \frac{\pi }{2}} \right)$$
D
$$y = 2\cos \left( {\frac{{10}}{3}t + \frac{\pi }{2}} \right)$$
Answer :
$$y = 2\sin \left( {\frac{{10}}{3}t - \frac{\pi }{2}} \right)$$
103.
What will be the force constant of the spring system shown in figure?
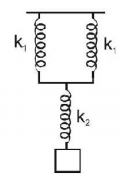
A
$$\frac{{{k_1}}}{2} + {k_2}$$
B
$${\left[ {\frac{1}{{2{k_1}}} + \frac{1}{{{k_2}}}} \right]^{ - 1}}$$
C
$$\left[ {\frac{1}{{2{k_1}}} + \frac{1}{{{k_2}}}} \right]$$
D
$${\left[ {\frac{2}{{{k_1}}} + \frac{1}{{{k_2}}}} \right]^{ - 1}}$$
Answer :
$${\left[ {\frac{1}{{2{k_1}}} + \frac{1}{{{k_2}}}} \right]^{ - 1}}$$
104. A simple harmonic wave having an amplitude $$a$$ and time period $$T$$ is represented by the equation $$y = 5\sin \pi \left( {t + 4} \right)m.$$ Then the value of amplitude $$\left( a \right)$$ in $$\left( m \right)$$ and time period $$\left( T \right)$$ in second are
A
$$a = 10,T = 2$$
B
$$a = 5,T = 1$$
C
$$a = 10,T = 1$$
D
$$a = 5,T = 2$$
Answer :
$$a = 5,T = 2$$
105. If a spring has time period $$T,$$ and is cut into $$n$$ equal parts, then the time period of each part will be
A
$$T\sqrt n $$
B
$$\frac{T}{{\sqrt n }}$$
C
$$nT$$
D
$$T$$
Answer :
$$\frac{T}{{\sqrt n }}$$
106. When a damped harmonic oscillator completes 100 oscillations, its amplitude is reduced to $$\frac{1}{3}$$ of its initial value. What will be its amplitude when it completes 200 oscillations ?
A
$$\frac{1}{5}$$
B
$$\frac{2}{3}$$
C
$$\frac{1}{6}$$
D
$$\frac{1}{9}$$
Answer :
$$\frac{1}{9}$$
107. A particle performs simple harmonic mition with amplitude $$A.$$ Its speed is trebled at the instant that it is at a distance $$\frac{{2A}}{3}$$ from equilibrium position. The new amplitude of the motion is
A
$$A\sqrt 3 $$
B
$$\frac{{7A}}{3}$$
C
$$\frac{A}{3}\sqrt {41} $$
D
$$3A$$
Answer :
$$\frac{{7A}}{3}$$
108. For a particle moving according to the equation $$x = a\cos \,\pi t,$$ the displacement in $$3\,s$$ is
A
0
B
$$0.5a$$
C
$$1.5a$$
D
$$2a$$
Answer :
$$2a$$
109. A cylindrical block of wood (density $$ = 650\,kg\,{m^{ - 3}}$$ ), of base area $$30\,c{m^2}$$ and height $$54\,cm,$$ floats in a liquid of density $$900\,kg\,{m^{ - 3}}.$$ The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly)
A
$$52\,cm$$
B
$$65\,cm$$
C
$$39\,cm$$
D
$$26\,cm$$
Answer :
$$39\,cm$$
110.
The oscillation of a body on a smooth horizontal surface is represented by the equation, where,
$$X = A\cos \left( {\omega t} \right)$$
$$X = $$ displacement at time $$t$$
$$\omega = $$ frequency of oscillation
Which one of the following graphs shows correctly the variation $$a$$ with $$t$$?
Here,
$$a$$ = acceleration at time $$t$$
$$T$$ = Time period
A


B


C


D


Answer :

