31.
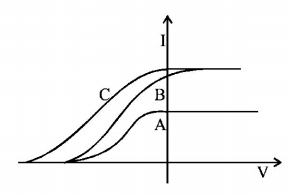
In a photoelectric experiment anode potential is plotted against plate current.
A
$$A$$ and $$B$$ will have different intensities while $$B$$ and $$C$$ will have different frequencies
B
$$B$$ and $$C$$ will have different intensities while $$A$$ and $$C$$ will have different frequencies
C
$$A$$ and $$B$$ will have different intensities while $$A$$ and $$C$$ will have equal frequencies
D
$$B$$ and $$C$$ will have equal intensities while $$A$$ and $$B$$ will have same frequencies
Answer :
$$B$$ and $$C$$ will have equal intensities while $$A$$ and $$B$$ will have same frequencies
32. The magnetic field in a travelling electromagnetic wave has a peak value of $$20\,nT.$$ The peak value of electric field strength is:
A
$$3\,V/m$$
B
$$6\,V/m$$
C
$$9\,V/m$$
D
$$12\,V/m$$
Answer :
$$6\,V/m$$
33. The anode voltage of a photocell is kept fixed. The wavelength $$\lambda $$ of the light falling on the cathode is gradually changed. The plate current $$I$$ of the photocell varies as follows
A


B


C


D


Answer :


34. Choose the correct statement :
A
In frequency modulation the amplitude of the high frequency carrier wave is made to vary in proportion to the amplitude of the audio signal.
B
In frequency modulation the amplitude of the high frequency carrier wave is made to vary in proportion to the frequency of the audio signal.
C
In amplitude modulation the amplitude of the high frequency carrier wave is made to vary in proportion to the amplitude of the audio signal.
D
In amplitude modulation the frequency of the high frequency carrier wave is made to vary in proportion to the amplitude of the audio signal.
Answer :
In amplitude modulation the amplitude of the high frequency carrier wave is made to vary in proportion to the amplitude of the audio signal.
35.
The electric field of light wave is given as
$$\eqalign{
& \overrightarrow E = {10^3}\cos \cr
& \left( {\frac{{2\pi x}}{{5 \times {{10}^{ - 7}}}} - 2\pi \times 6 \times {{10}^{14}}t} \right)\hat x\frac{N}{C} \cr} $$
This light falls on a metal plate of work function $$2eV.$$ The stopping potential of the photo-electrons is:
Given, $$E\left( {{\text{in}}\,eV} \right) = \frac{{12375}}{{\lambda \left( {{\text{in}}\,\mathop A\limits^ \circ } \right)}}$$
A
$$2.0\,V$$
B
$$0.72\,V$$
C
$$0.48\,V$$
D
$$2.48\,V$$
Answer :
$$0.48\,V$$
36.
Surface of certain metal is first illuminated with light of wavelength $${\lambda _1} = 350\,nm$$ and then, by light of wavelength $${\lambda _2} = 540\,nm.$$ It is found that the maximum speed of the photo electrons in the two cases differ by a factor of (2) The work function of the metal (in $$eV$$ ) is close to:
(Energy of photon $$ = \frac{{1240}}{{\lambda \left( {{\text{in}}\,nm} \right)}}eV$$ )
A
1.8
B
2.5
C
5.6
D
1.4
Answer :
1.8
37. If a source of power $$4kW$$ produces $${10^{20}}$$ photons/second, the radiation belongs to a part of the spectrum called
A
X-rays
B
ultraviolet rays
C
microwaves
D
$$\gamma $$ -rays
Answer :
X-rays
38. A signal $$A\cos \omega t$$ is transmitted using $${v_0}\sin \omega $$ modulated $$\left( {AM} \right)$$ signal is:
A
$${v_0}\sin {\omega _0}t + \frac{A}{2}\sin \left( {{\omega _0} - \omega } \right)t + \frac{A}{2}\left( {{\omega _0} + \omega } \right)t$$
B
$${v_0}\sin \left[ {{\omega _0}\left( {1 + 0.01A\sin \omega t} \right)t} \right]$$
C
$${v_0}\sin {\omega _0}t + A\cos \omega t$$
D
$$\left( {{v_0} + A} \right)\cos \omega t\sin {\omega _0}t$$
Answer :
$${v_0}\sin {\omega _0}t + \frac{A}{2}\sin \left( {{\omega _0} - \omega } \right)t + \frac{A}{2}\left( {{\omega _0} + \omega } \right)t$$
39. A photoelectric material having work-function $${\phi _0}$$ is illuminated with light of wavelength $$\lambda \left( {\lambda < \frac{{hc}}{{{\phi _0}}}} \right).$$ The fastest photoelectron has a de-Broglie wavelength $${\lambda _d}.$$ A change in wavelength of the incident light by $$\Delta \lambda $$ result in a change $$\Delta {\lambda _d}$$ in $${\lambda _d}.$$ Then the ratio $$\frac{{\Delta {\lambda _d}}}{{\Delta \lambda }}$$ is proportional to
A
$$\frac{{{\lambda _d}}}{\lambda }$$
B
$$\frac{{\lambda _d^2}}{{{\lambda ^2}}}$$
C
$$\frac{{\lambda _d^3}}{\lambda }$$
D
$$\frac{{\lambda _d^3}}{{{\lambda ^2}}}$$
Answer :
$$\frac{{\lambda _d^3}}{{{\lambda ^2}}}$$
40. Photoelectric effect experiments are performed using three different metal plates $$p,\,q$$ and $$r$$ having work functions $${\phi _p} = 2.0\,eV,{\phi _q} = 2.5\,eV$$ and $${\phi _r} = 3.0\,eV$$ respectively. A light beam containing wavelengths of $$550\,nm, 450 nm$$ and $$350\,nm$$ with equal intensities illuminates each of the plates. The correct $$I-V$$ graph for the experiment is [Take $$hc = 1240\,eV\,nm$$ ]
A


B


C


D


Answer :


