11. Suppose potential energy between electron and proton at separation $$r$$ is given by $$U = K\ln \left( r \right),$$ where $$K$$ is a constant. For such a hypothetical hydrogen atom, the ratio of energy difference between energy levels ($$n = 1$$ and $$n= 2$$ ) and ($$n=2$$ and $$n=4$$ ) is
A
1
B
2
C
3
D
4
Answer :
1
12. When hydrogen atom is in its first excited level, its radius is
A
four times, its ground state radius
B
twice, its ground state radius
C
same as its ground sate radius
D
half of its ground state radius
Answer :
four times, its ground state radius
13. The ionisation energy of hydrogen atom is $$13.6\,eV.$$ Following Bohr’s theory, the energy corresponding to a transition between 3rd and 4th orbit is
A
$$3.40\,eV$$
B
$$1.51\,eV$$
C
$$0.85\,eV$$
D
$$0.66\,eV$$
Answer :
$$0.66\,eV$$
14. In a hydrogen like atom electron make transition from an energy level with quantum number $$n$$ to another with quantum number $$\left( {n - 1} \right).$$ If $$n>>1,$$ the frequency of radiation emitted is proportional to :
A
$$\frac{1}{n}$$
B
$$\frac{1}{{{n^2}}}$$
C
$$\frac{1}{{\frac{{{n^3}}}{2}}}$$
D
$$\frac{1}{{{n^3}}}$$
Answer :
$$\frac{1}{{{n^3}}}$$
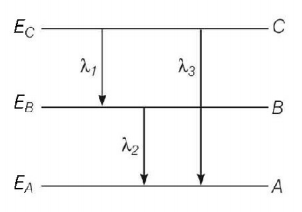
15. Energy levels $$A,B,C$$ of a certain atom correspond to increasing values of energy i.e. $${E_A} < {E_B} < {E_C}.$$ If $${\lambda _1},{\lambda _2},{\lambda _3}$$ are the wavelengths of radiation corresponding to the transitions $$C$$ to $$B,B$$ to $$A$$ and $$C$$ to $$A$$ respectively, which of the following relation is correct ?
A
$${\lambda _3} = {\lambda _1} + {\lambda _2}$$
B
$${\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$$
C
$${\lambda _1} + {\lambda _2} + {\lambda _3} = 0$$
D
$$\lambda _3^2 = \lambda _1^2 + \lambda _2^2$$
Answer :
$${\lambda _3} = \frac{{{\lambda _1}{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}$$
16. If an electron in a hydrogen atom jumps from the 3rd orbit to the 2nd orbit, it emits a photon of wavelength $$\lambda .$$ When it jumps from the 4th orbit to the 3rd orbit, the corresponding wavelength of the photon will be
A
$$\frac{{16}}{{25}}\lambda $$
B
$$\frac{9}{{16}}\lambda $$
C
$$\frac{{20}}{7}\lambda $$
D
$$\frac{{20}}{{13}}\lambda $$
Answer :
$$\frac{{20}}{7}\lambda $$
17.
If radiation corresponding to first line of "Balmer series" of $$H{e^ + }$$ ion knocked out electron from 1st excited state of $$H$$ atom, the kinetic energy of ejected electron from $$H$$ atom would be $$\left( {eV} \right) - $$
[Given $${E_n} = - \frac{{{Z^2}}}{{{n^2}}}\left( {13.6\,eV} \right)$$ ]
A
$$4.155\,eV$$
B
$$8.310\,eV$$
C
$$2.515\,eV$$
D
$$5.550\,eV$$
Answer :
$$4.155\,eV$$
18. An electron in a hydrogen atom makes a transition from $$n = {n_1}$$ to $$n = {n_2}.$$ The time period of electron in the initial state is eight times that in the final state. Then which of the following statement is true ?
A
$${n_1} = 3{n_2}$$
B
$${n_1} = 4{n_2}$$
C
$${n_1} = 2{n_2}$$
D
$${n_1} = 5{n_2}$$
Answer :
$${n_1} = 2{n_2}$$
19. In a hydrogen like atom electron make transition from an energy level with quantum number $$n$$ to another with quantum number $$\left( {n - 1} \right).$$ If $$n > > 1,$$ the frequency of radiation emitted is proportional to :
A
$$\frac{1}{n}$$
B
$$\frac{1}{{{n^2}}}$$
C
$$\frac{1}{{\frac{{{n^3}}}{2}}}$$
D
$$\frac{1}{{{n^3}}}$$
Answer :
$$\frac{1}{{{n^3}}}$$
20. In the Bohr model of a hydrogen atom, the centripetal force is furnished by the coulomb attraction between the proton and the electron. If $${a_0}$$ is the radius of the ground state orbit, $$m$$ is the mass, $$e$$ is the charge on the electron and $${\varepsilon _0}$$ is the vacuum permittivity, the speed of the electron is
A
$$0$$
B
$$\frac{e}{{\sqrt {{\varepsilon _0}{a_0}m} }}$$
C
$$\frac{e}{{\sqrt {4\pi {\varepsilon _0}{a_0}m} }}$$
D
$$\frac{{\sqrt {4\pi {\varepsilon _0}{a_0}m} }}{e}$$
Answer :
$$\frac{e}{{\sqrt {4\pi {\varepsilon _0}{a_0}m} }}$$