31. If the potential of a capacitor having Capacity $$6\,\mu F$$ is increased from $$10\,V$$ to $$20\,V,$$ then increase in its energy will be
A
$$4 \times {10^{ - 4}}\,J$$
B
$$4 \times {10^{ - 14}}\,J$$
C
$$9 \times {10^{ - 4}}\,J$$
D
$$12 \times {10^{ - 6}}\,J$$
Answer :
$$9 \times {10^{ - 4}}\,J$$
32. The electric potential at a point in free space due to a charge $$Q$$ coulomb is $$Q \times {10^{11}}V.$$ The electric field at that point is
A
$$4\pi {\varepsilon _0}\,Q \times {10^{22}}\,V/m$$
B
$$12\pi {\varepsilon _0}\,Q \times {10^{20}}\,V/m$$
C
$$4\pi {\varepsilon _0}\,Q \times {10^{20}}\,V/m$$
D
$$12\pi {\varepsilon _0}\,Q \times {10^{22}}\,V/m$$
Answer :
$$4\pi {\varepsilon _0}\,Q \times {10^{22}}\,V/m$$
33. A hollow metal sphere of radius $$5\,cm$$ is charged such that the potential on its surface is $$10\,V.$$ The potential at a distance of $$2\,cm$$ from the centre of the sphere is
A
zero
B
$$10\,V$$
C
$$4\,V$$
D
$$\frac{{10}}{3}\,V$$
Answer :
$$10\,V$$
34. Identical charges $$\left( { - q} \right)$$ are placed at each corners of a cube of side $$b,$$ then the electrostatic potential energy of charge $$\left( { + q} \right)$$ placed at the centre of the cube will be
A
$$ - \frac{{4\sqrt 2 {q^2}}}{{\pi {\varepsilon _0}}}$$
B
$$\frac{{8\sqrt 2 {q^2}}}{{\pi {\varepsilon _0}b}}$$
C
$$ - \frac{{4{q^2}}}{{\sqrt 3 \pi {\varepsilon _0}b}}$$
D
$$\frac{{8\sqrt 2 {q^2}}}{{4\pi {\varepsilon _0}b}}$$
Answer :
$$ - \frac{{4{q^2}}}{{\sqrt 3 \pi {\varepsilon _0}b}}$$
35. The potential at a point $$x$$ (measured in $$\mu m$$ ) due to some charges situated on the $$x$$-axis is given by $$V\left( x \right) = \frac{{20}}{{\left( {{x^2} - 4} \right)}}volt.$$ The electric field $$E$$ at $$x = 4\,\mu m$$ is given by
A
$$\left( {\frac{{10}}{9}} \right)volt/\mu m$$ in the $$+ve$$ $$x$$ direction
B
$$\left( {\frac{{5}}{3}} \right)volt/\mu m$$ in the $$-ve$$ $$x$$ direction
C
$$\left( {\frac{{5}}{3}} \right)volt/\mu m$$ in the $$+ve$$ $$x$$ direction
D
$$\left( {\frac{{10}}{9}} \right)volt/\mu m$$ in the $$-ve$$ $$x$$ direction
Answer :
$$\left( {\frac{{10}}{9}} \right)volt/\mu m$$ in the $$+ve$$ $$x$$ direction
36. The electric potential at a point $$\left( {x,y,z} \right)$$ is given by $$V = - {x^2}y - x{z^3} + 4.$$ The electric field $${\vec E}$$ at that point is
A
$$\vec E = \hat i\,2xy + \hat j\left( {{x^2} + {y^2}} \right) + \hat k\left( {3xz - {y^2}} \right)$$
B
$$\vec E = \hat i\,{z^3} + \hat j\,xyz + \hat k\,{z^2}$$
C
$$\vec E = \hat i\left( {\,2xy - {z^3}} \right) + \hat j\,x{y^2} + \hat k\,3{z^2}x$$
D
$$\vec E = \hat i\left( {\,2xy - {z^3}} \right) + \hat j\,{x^2} + \hat k\,3x{z^2}$$
Answer :
$$\vec E = \hat i\left( {\,2xy - {z^3}} \right) + \hat j\,{x^2} + \hat k\,3x{z^2}$$
37. Two points $$P$$ and $$Q$$ are maintained at the potentials of $$10\,V$$ and $$- 4\,V,$$ respectively. The work done in moving 100 electrons from $$P$$ to $$Q$$ is:
A
$$9.60 \times {10^{ - 17}}J$$
B
$$ - 2.24 \times {10^{ - 16}}J$$
C
$$2.24 \times {10^{ - 16}}J$$
D
$$ - 9.60 \times {10^{ - 17}}J$$
Answer :
$$2.24 \times {10^{ - 16}}J$$
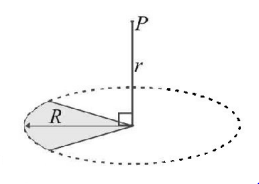
38.
A plastic disc is charged on one side with a uniform surface charge density $$\sigma $$ and then three quadrant of the disk are removed. The remaining quadrant is shown in figure, with $$V = 0$$ at infinity, the potential due to the remaining quadrant at point $$P$$ is
A
$$\frac{\sigma }{{2{ \in _0}}}\left[ {{{\left( {{r^2} + R} \right)}^{\frac{1}{2}}} - r} \right]$$
B
$$\frac{\sigma }{{2{ \in _0}}}\left[ {R - r} \right]$$
C
$$\frac{\sigma }{{8{ \in _0}}}\left[ {{{\left( {{r^2} + {R^2}} \right)}^{\frac{1}{2}}} - r} \right]$$
D
None of these
Answer :
$$\frac{\sigma }{{8{ \in _0}}}\left[ {{{\left( {{r^2} + {R^2}} \right)}^{\frac{1}{2}}} - r} \right]$$
39. There is an infinite straight chain of alternating charges $$q$$ and $$-q.$$ The distance between the two neighbouring charges is equal to $$a.$$ Find the interaction energy of any charge with all the other charges.
A
$$ - \frac{{2{q^2}}}{{4\pi {\varepsilon _0}a}}$$
B
$$\frac{{2{q^2}{{\log }_e}2}}{{4\pi {\varepsilon _0}a}}$$
C
$$ - \frac{{2{q^2}{{\log }_e}2}}{{4\pi {\varepsilon _0}a}}$$
D
None of these
Answer :
$$ - \frac{{2{q^2}{{\log }_e}2}}{{4\pi {\varepsilon _0}a}}$$
40. A bullet of mass $$2\,g$$ is having a charge of $$2\mu C.$$ Through what potential difference must it be accelerated, starting from rest, to acquire a speed of $$10\,m/s$$ ?
A
$$5\,kV$$
B
$$50\,kV$$
C
$$5\,V$$
D
$$50\,V$$
Answer :
$$50\,kV$$
