21. The electric field intensity at all points in space is given by $$\vec E = \sqrt 3 \hat i - \hat j\,{\text{volt/metre}}{\text{.}}$$ The nature of equipotential lines in $$xy$$ -plane is given by
A


B


C


D


Answer :


22. A point charge of magnitude $$ + 1\mu C$$ is fixed at $$\left( {0,0,0} \right).$$ An isolated uncharged spherical conductor, is fixed with its center at $$\left( {4,0,0} \right).$$ The potential and the induced electric field at the centre of the sphere is :
A
$$1.8 \times {10^5}\,V$$ and $$ - 5.625 \times {10^6}\,V/m$$
B
$$0\,V$$ and $$0\,V/m$$
C
$$2.25 \times {10^5}V$$ and $$ - 5.625 \times {10^6}\,V/m$$
D
$$2.25 \times {10^5}V$$ and $$0\,V/m$$
Answer :
$$2.25 \times {10^5}V$$ and $$ - 5.625 \times {10^6}\,V/m$$
23. A hollow metal sphere of radius $$10\,cm$$ is charged such that the potential on its surface is $$80\,V.$$ The potential at the centre of the sphere is
A
zero
B
$$80\,V$$
C
$$800\,V$$
D
$$8\,V$$
Answer :
$$80\,V$$
24.
Four electric charges $$ + q, + q, - q$$ and $$- q$$ are placed at the corners of a square of side $$2L$$ (see figure). The electric potential at point $$A,$$ mid-way between the two charges $$+q$$ and $$+q$$ is

A
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 + \frac{1}{{\sqrt 5 }}} \right)$$
B
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)$$
C
zero
D
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 + \sqrt 5 } \right)$$
Answer :
$$\frac{1}{{4\pi {\varepsilon _0}}}\frac{{2q}}{L}\left( {1 - \frac{1}{{\sqrt 5 }}} \right)$$
25.
Figure shows a system of three concentric metal shells $$A,B$$ and $$C$$ with radii $$a,2a$$ and $$3a$$ respectively. Shell $$B$$ is earthed and shell $$C$$ is given a charge $$Q.$$ Now if shell $$C$$ is connected to shell $$A,$$ then the final charge on the shell $$B,$$ is equal to

A
$$ - \frac{{4Q}}{{13}}$$
B
$$ - \frac{{8Q}}{{11}}$$
C
$$ - \frac{{5Q}}{3}$$
D
$$ - \frac{{3Q}}{7}$$
Answer :
$$ - \frac{{8Q}}{{11}}$$
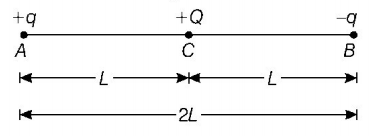
26.
Charges $$+ q$$ and $$- q$$ are placed at points $$A$$ and $$B$$ respectively which are a distance $$2L$$ apart, $$C$$ is the midpoint between $$A$$ and $$B.$$ The work done in moving a charge $$+Q$$ along the semicircle $$CRD$$ is

A
$$\frac{{qQ}}{{4\pi {\varepsilon _0}L}}$$
B
$$\frac{{qQ}}{{2\pi {\varepsilon _0}L}}$$
C
$$\frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
D
$$ - \frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
Answer :
$$ - \frac{{qQ}}{{6\pi {\varepsilon _0}L}}$$
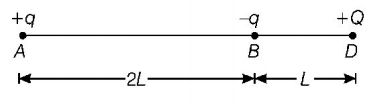
27. A charge $$+q$$ fixed at each of the points $$x = {x_0},x = 3{x_0},x = 5{x_0},...$$ upto $$\infty $$ on $$X$$-axis and charge $$-q$$ is fixed on each of the points $$x = 2{x_0},x = 4{x_0},...$$ upto $$\infty .$$ Here $${x_0}$$ is a positive constant. Take the potential at a point due to a charge $$Q$$ at a distance $$r$$ form it to be $$\frac{Q}{{4\pi {\varepsilon _0}r}},$$ then the potential at the origin due to above system of charges will be:
A
zero
B
infinite
C
$$\frac{q}{{8\pi {\varepsilon _0}{x_0}{{\log }_e}2}}$$
D
$$\frac{{q{{\log }_e}2}}{{4\pi {\varepsilon _0}{x_0}}}$$
Answer :
$$\frac{{q{{\log }_e}2}}{{4\pi {\varepsilon _0}{x_0}}}$$
28. Four charges $${q_1} = 2 \times {10^{ - 8}}C,{q_2} = - 2 \times {10^{ - 8}}C,{q^3} = - 3 \times {10^{ - 8}}C,$$ and $${q_4} = 6 \times {10^{ - 8}}C$$ are placed at four corners of a square of side $$\sqrt 2 \,m.$$ What is the potential at the centre of the square?
A
$$270\,V$$
B
$$300\,V$$
C
Zero
D
$$100\,V$$
Answer :
$$270\,V$$
29. $$A$$ and $$B$$ are two points in an electric field. If the work done in carrying $$4.0\,C$$ of electric charge from $$A$$ to $$B$$ is $$16.0\,J,$$ the potential difference between $$A$$ and $$B$$ is
A
zero
B
$$2.0\,V$$
C
$$4.0\,V$$
D
$$16.0\,V$$
Answer :
$$4.0\,V$$
30. The electric potential at a point $$\left( {x,y} \right)$$ in the $$x-y$$ plane is given by $$V = - kxy.$$ The field intensity at a distance $$r$$ from the origin varies as
A
$${r^2}$$
B
$$r$$
C
$$\frac{1}{r}$$
D
$$\frac{1}{{{r^2}}}$$
Answer :
$$r$$