11.
$$A,B$$ and $$C$$ are three points in a uniform electric field. The electric potential is

A
maximum at $$B$$
B
maximum at $$C$$
C
same at all the three points $$A,B$$ and $$C$$
D
maximum at $$A$$
Answer :
maximum at $$B$$
12. Three concentric spherical shells have radii $$a,b$$ and $$c\left( {a < b < c} \right)$$ and have surface charge densities $$\sigma , - \sigma $$ and $$\sigma $$ respectively. If $${V_A},{V_B}$$ and $${V_C}$$ denote the potentials of the three shells, then for $$c = a + b,$$ we have
A
$${V_C} = {V_A} \ne {V_B}$$
B
$${V_C} = {V_B} \ne {V_A}$$
C
$${V_C} \ne {V_B} \ne {V_A}$$
D
$${V_C} = {V_B} = {V_A}$$
Answer :
$${V_C} = {V_B} = {V_A}$$
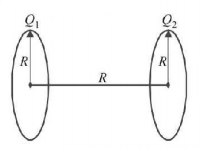
13. Two identical thin rings each of radius $$R$$ meters are coaxially placed at a distance $$R$$ meters apart. If $${Q_1}$$ coulomb and $${Q_2}$$ coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge $$q$$ from the centre of one ring to that of other is
A
zero
B
$$\frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
C
$$\frac{{q\sqrt 2 \left( {{Q_1} + {Q_2}} \right)}}{{4\pi {\varepsilon _0}R}}$$
D
$$\frac{{q\left( {{Q_1} + {Q_2}} \right)\left( {\sqrt 2 + 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
Answer :
$$\frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
14. Some charge is being given to a conductor, then its potential is
A
maximum at surface
B
maximum at centre
C
same throughout the conductor
D
maximum somewhere between surface and centre
Answer :
same throughout the conductor
15. Three concentric charged metallic spherical shells $$A,B$$ and $$C$$ have radii $$a,b$$ and $$c;$$ charge densities $$\sigma , - \sigma $$ and $$\sigma $$ and potentials $${V_A},{V_B}$$ and $${V_C}$$ respectively. Then which of the following relations is correct?
A
$${V_A} = \left( {a + b + c} \right)\frac{\sigma }{{{\varepsilon _0}}}$$
B
$${V_B} = \left( {\frac{{{a^2}}}{b} - b + c} \right)\frac{\sigma }{{{\varepsilon _0}}}$$
C
$${V_C} = \left( {\frac{{{a^2} + {b^2}}}{b} + c} \right)\frac{\sigma }{{{\varepsilon _0}}}$$
D
$${V_A} = {V_B} = {V_C} = \left( {a + b + c} \right)\frac{\sigma }{{{\varepsilon _0}}}$$
Answer :
$${V_B} = \left( {\frac{{{a^2}}}{b} - b + c} \right)\frac{\sigma }{{{\varepsilon _0}}}$$
16. Three identical particles, each possessing the mass $$m$$ and charge $$+q,$$ are placed at the corners of an equilateral triangle with side $${r_0}.$$ The particles are simultaneously set free and start flying apart symmetrically due to Coulomb’s repulsion forces. The work performed by Coulomb’s forces acting on each particle until the particles fly from one another to a very large distance is (where $$k = \frac{1}{{4\pi {\varepsilon _0}}}.$$ )
A
$$\frac{{3k{q^2}}}{{{r_0}}}$$
B
$$\frac{{k{q^2}}}{{{r_0}}}$$
C
$$\frac{{3k{q^2}}}{{2{r_0}}}$$
D
$$\frac{{k{q^2}}}{{2{r_0}}}$$
Answer :
$$\frac{{k{q^2}}}{{{r_0}}}$$
17. In a region, the potential is represented by $$V\left( {x,y,z} \right) = 6x - 8xy - 8y + 6yz,$$ where $$V$$ is in volts and $$x,y,z$$ are in metres. The electric force experienced by a charge of $$2C$$ situated at point $$\left( {1,1,1} \right)$$ is
A
$$6\sqrt 5 N$$
B
$$30\,N$$
C
$$24\,N$$
D
$$4\sqrt {35} \,N$$
Answer :
$$4\sqrt {35} \,N$$
18.
An electron having charge $$e$$ and mass $$m$$ starts from the lower plate of two metallic plates separated by a distance $$d.$$ If the potential difference between the plates is $$V,$$ the time taken by the electron to reach the upper plate is given by

A
$$\sqrt {\frac{{2m{d^2}}}{{eV}}} $$
B
$$\sqrt {\frac{{m{d^2}}}{{eV}}} $$
C
$$\sqrt {\frac{{m{d^2}}}{{2eV}}} $$
D
$$\frac{{2m{d^2}}}{{eV}}$$
Answer :
$$\sqrt {\frac{{2m{d^2}}}{{eV}}} $$
19.
Figure shows a system of three positive charges placed at the vertices of an equilateral triangle. To decrease the potential energy of the system,

A
a positive charge should be placed at centroid.
B
a negative charge should be placed at centroid.
C
distance between the charges should be decreased.
D
it should be rotated by an angle of $$\frac{\pi }{2}$$ radian.
Answer :
distance between the charges should be decreased.
20. A non-conducting ring of radius $$0.5\,m$$ carries a total charge of $$1.11 \times {10^{ - 10}}C$$ distributed non-uniformly on its circumference producing an electric field $$E$$ everywhere in space. The value of the integral $$\int\limits_{\ell \, = \,\infty }^{\ell \, = \,0} { - E.d\ell } $$ ($$\ell \, = \,0$$ being center of the ring) in volts is
A
$$+ 2$$
B
$$- 1$$
C
$$- 2$$
D
zero
Answer :
$$+ 2$$