21.
Two identical beads of $$m = 100\,gram$$ are connected by an inextensible massless string can slide along the two arms $$AC$$ and $$BC$$ of a rigid smooth wire frame in a vertical plane. If the system is released from rest, the kinetic energy of the first particle when they have moved by a distance of $$0.1\,m$$ is $$8x \times {10^{ - 3}}J.$$ Find the value of $$x.\left( {g = 10\,m/{s^2}} \right)$$

A
8
B
6
C
9
D
11
Answer :
8
22. A body of mass $$m$$ is accelerated uniformly from rest to a speed $$v$$ in a time $$T.$$ The instantaneous power delivered to the body as a function of time is given by
A
$$\frac{{m{v^2}}}{{{T^2}}}.{t^2}$$
B
$$\frac{{m{v^2}}}{{{T^2}}}.t$$
C
$$\frac{1}{2}\frac{{m{v^2}}}{{{T^2}}}.{t^2}$$
D
$$\frac{1}{2}\frac{{m{v^2}}}{{{T^2}}}.t$$
Answer :
$$\frac{{m{v^2}}}{{{T^2}}}.t$$
23. A time dependent force $$F = 6t$$ acts on a particle of mass $$1 \,kg.$$ If the particle starts from rest, the work done by the force during the first $$1 \,second$$ will be-
A
$$9\,J$$
B
$$18\,J$$
C
$$4.5\,J$$
D
$$22\,J$$
Answer :
$$4.5\,J$$
24. A shell of mass $$200\,g$$ is ejected from a gun of mass $$4\,kg$$ by an explosion that generates $$1.05\,kJ$$ of energy. The initial velocity of the shell is
A
$$100\,m{s^{ - 1}}$$
B
$$80\,m{s^{ - 1}}$$
C
$$40\,m{s^{ - 1}}$$
D
$$120\,m{s^{ - 1}}$$
Answer :
$$100\,m{s^{ - 1}}$$
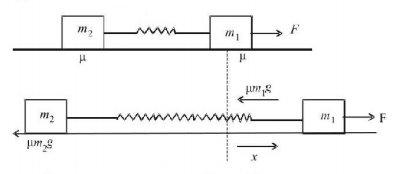
25. Two blocks of masses $${m_1} = 10\,kg$$ and $${m_2} = 20\,kg$$ are connected by a spring of stiffness $$k = 200\,N/m.$$ The coefficient of friction between the blocks and the fixed horizontal surface is $$\mu = 0.1.$$ Find the minimum constant horizontal force $$F$$ (in newtons) to be applied to $${m_1}$$ in order to slide the mass $${m_2}.$$
A
$$\mu {m_1}g + \frac{{\mu {m_2}g}}{2}$$
B
$$\mu {m_1}g + \mu {m_2}g$$
C
$$\mu {m_1}g - \frac{{\mu {m_2}g}}{2}$$
D
$$\frac{{\mu {m_1}g + \mu {m_2}g}}{2}$$
Answer :
$$\mu {m_1}g + \frac{{\mu {m_2}g}}{2}$$
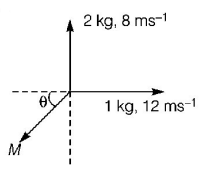
26. An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, $$1\,kg$$ first part moving with a velocity of $$12\,m{s^{ - 1}}$$ and $$2\,kg$$ second part moving with a velocity of $$8\,m{s^{ - 1}}.$$ If the third part flies off with a velocity of $$4\,m{s^{ - 1}},$$ its mass would be
A
$$5\,kg$$
B
$$7\,kg$$
C
$$17\,kg$$
D
$$3\,kg$$
Answer :
$$5\,kg$$
27. When a body is projected vertically up from the ground with certain velocity, its potential energy and kinetic energy at a point $$A$$ are in the ratio $$2 : 3.$$ If the same body is projected with double the previous velocity, then at the same point $$A$$ the ratio of its potential energy to kinetic energy is
A
$$9:1$$
B
$$2:9$$
C
$$1:9$$
D
$$9:2$$
Answer :
$$1:9$$
28. If kinetic energy of a body is increased by $$300\% ,$$ then percentage change in momentum will be
A
$$100\% $$
B
$$150\% $$
C
$$265\% $$
D
$$73.2\% $$
Answer :
$$100\% $$
29.
The figure gives the potential energy function $$U\left( x \right)$$ for a system in which a particle is in one-dimensional motion. In which region the magnitude of the force on the particle is greatest :

A
$$OA$$
B
$$AB$$
C
$$BC$$
D
$$CD$$
Answer :
$$CD$$
30. A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement $$x$$ is proportional to-
A
$$x$$
B
$${e^x}$$
C
$${x^2}$$
D
$${\log _e}x$$
Answer :
$${x^2}$$