21. A particle of mass $$m$$ rotates with a uniform angular speed $$\omega .$$ It is viewed from a frame rotating about the $$z$$-axis with a uniform angular velocity $${\omega _0}.$$ The centrifugal force on the particle is :
A
$$m{\omega ^2}r$$
B
$$m\omega _0^2r$$
C
$$m\left( {\frac{{\omega + {\omega _0}}}{2}} \right)a$$
D
zero
Answer :
$$m\omega _0^2r$$
22. One end of the string of length $$l$$ is connected to a particle of mass $$m$$ and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed $$v,$$ the net force on the particle (directed towards center) will be ($$T$$ represents the tension in the string)
A
$$T$$
B
$$T + \frac{{m{v^2}}}{l}$$
C
$$T - \frac{{m{v^2}}}{l}$$
D
Zero
Answer :
$$T$$
23.
A uniform rod $$AB$$ of length $$3r$$ remains in equilibrium on a hemispherical bowl of radius $$r$$ as shown in figure. Ignoring friction, the inclination of the rod $$\theta $$ with the horizontal is
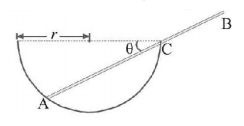
A
$${\cos ^{ - 1}}\left( {\frac{1}{3}} \right)$$
B
$${\sin ^{ - 1}}\left( {\frac{1}{3}} \right)$$
C
$${\cos ^{ - 1}}\left( {0.9} \right)$$
D
$${\sin ^{ - 1}}\left( {0.9} \right)$$
Answer :
$${\cos ^{ - 1}}\left( {0.9} \right)$$
24. A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, then the maximum friction of the length of the chain that can hang over one edge of the table is
A
$$20\% $$
B
$$25\% $$
C
$$35\% $$
D
$$15\% $$
Answer :
$$20\% $$
25.
A mass $$'m'$$ is supported by a massless string wound around a uniform hollow cylinder of mass $$m$$ and radius $$R.$$ If the string does not slip on the cylinder, with what acceleration will the mass fall or release?

A
$$\frac{{2g}}{3}$$
B
$$\frac{g}{2}$$
C
$$\frac{{5g}}{6}$$
D
$$g$$
Answer :
$$\frac{g}{2}$$
26. A particle is moving with a uniform speed in a circular orbit of radius $$R$$ in a central force inversely proportional to the $${n^{th}}$$ power of $$R.$$ If the period of rotation of the particle is $$T,$$ then:
A
$$T \propto {R^{\frac{3}{2}}}\,{\text{for}}\,{\text{any}}\,n.$$
B
$$T \propto {R^{\frac{n}{{2 + 1}}}}$$
C
$$T \propto {R^{\frac{{\left( {n + 1} \right)}}{2}}}$$
D
$$T \propto {R^{\frac{n}{2}}}$$
Answer :
$$T \propto {R^{\frac{{\left( {n + 1} \right)}}{2}}}$$