41. A spring of force constant $$k$$ is cut into lengths of ratio $$1:2:3.$$ They are connected in series and the new force constant is $$k'.$$ If they are connected in parallel and force constant is $$k'',$$ then 1 $$k':k''$$ is
A
$$1:6$$
B
$$1:9$$
C
$$1:11$$
D
$$1:14$$
Answer :
$$1:11$$
42. When forces $${F_1},{F_2},{F_3}$$ are acting on a particle of mass $$m$$ such that $${F_2}$$ and $${F_3}$$ are mutually perpendicular, then the particle remains stationary. If the force $${F_1}$$ is now removed then the acceleration of the particle is
A
$$\frac{{{F_1}}}{m}$$
B
$$\frac{{{F_2}{F_3}}}{{m{F_1}}}$$
C
$$\frac{{\left( {{F_2} - {F_3}} \right)}}{m}$$
D
$$\frac{{{F_2}}}{m}$$
Answer :
$$\frac{{{F_1}}}{m}$$
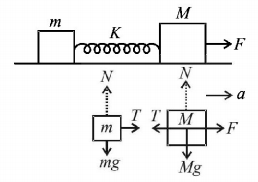
43. A block of mass $$m$$ is connected to another block of mass $$M$$ by a spring (massless) of spring constant $$k.$$ The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force $$F$$ starts acting on the block of mass $$M$$ to pull it. Find the force of the block of mass $$m.$$
A
$$\frac{{MF}}{{\left( {m + M} \right)}}$$
B
$$\frac{{mF}}{M}$$
C
$$\frac{{\left( {M + m} \right)F}}{m}$$
D
$$\frac{{mF}}{{\left( {m + M} \right)}}$$
Answer :
$$\frac{{mF}}{{\left( {m + M} \right)}}$$
44.
A mass of $$1\,kg$$ is suspended by a thread. It is
1. lifted up with an acceleration $$4.9\,m/{s^2},$$
2. lowered with an acceleration $$4.9\,m/{s^2}.$$
The ratio of the tensions is
A
$$3:1$$
B
$$1:3$$
C
$$1:2$$
D
$$2:1$$
Answer :
$$3:1$$
45.
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle $$\theta $$ should be

A
$${0^ \circ }$$
B
$${30^ \circ }$$
C
$${45^ \circ }$$
D
$${60^ \circ }$$
Answer :
$${45^ \circ }$$
46. A block $$A$$ of mass $$4\,kg$$ is placed on another block $$B$$ of mass $$5\,kg,$$ and the block $$B$$ rests on a smooth horizontal table. If the minimum force that can be applied on $$A$$ so that both the blocks move together is $$12\,N,$$ the maximum force that can be applied to $$B$$ for the blocks to move together will be:
A
$$30\,N$$
B
$$25\,N$$
C
$$27\,N$$
D
$$48\,N$$
Answer :
$$27\,N$$
47. A light spring balance hangs from the hook of the other light spring balance and a block of mass $$M\,kg$$ hangs from the former one. Then the true statement about the scale reading is
A
Both the scales read $$M\,kg$$ each
B
The scale of the lower one reads $$M\,kg$$ and of the upper one zero
C
The reading of the two scales can be anything but the sum of the reading will be $$M\,kg$$
D
Both the scales read $$\frac{M}{2}kg$$ each
Answer :
Both the scales read $$M\,kg$$ each
48. A particle moves in the $$X - Y$$ plane under the influence of a force such that its linear momentum is $$\vec p(t) = A[\hat i\cos (kt) - \hat j\sin (kt)],$$ where $$A$$ and $$k$$ are constants. The angle between the force and the momentum is
A
$${0^ \circ }$$
B
$${30^ \circ }$$
C
$${45^ \circ }$$
D
$${90^ \circ }$$
Answer :
$${90^ \circ }$$
49. A ship of mass $$3 \times {10^7}\,kg$$ initially at rest, is pulled by a force of $$5 \times {10^4}\,N$$ through a distance of $$3m.$$ Assuming that the resistance due to water is negligible, the speed of the ship is
A
$$1.5 m/sec.$$
B
$$60 m/sec.$$
C
$$0.1 m/sec.$$
D
$$5 m/sec.$$
Answer :
$$0.1 m/sec.$$
50.
In the figure (i) an extensible string is fixed at one end and the other end is pulled by a tension $$T.$$ In figure (ii) another identical string is pulled by tension $$T$$ at both the ends. The ratio of elongation in equilibrium of string in (i) to the elongation of string in (ii) is

A
$$1:1$$
B
$$1:2$$
C
$$2:1$$
D
0
Answer :
$$1:1$$