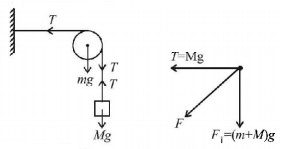
31.
For the given situation as shown in the figure, the value of $$\theta $$ to keep the system in equilibrium will be

A
$${30^ \circ }$$
B
$${45^ \circ }$$
C
$${0^ \circ }$$
D
$${90^ \circ }$$
Answer :
$${45^ \circ }$$
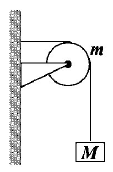
32.
A string of negligible mass going over a damped pulley of mass $$m$$ supports a block of mass $$M$$ as shown in the figure. The force on the pulley by the clamp is given by
A
$$\sqrt 2 \,{\text{Mg}}$$
B
$$\sqrt 2 \,{\text{mg}}$$
C
$$\sqrt {{{\left( {M + m} \right)}^2} + {m^2}} g$$
D
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
Answer :
$$\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} g$$
33.
Two blocks of mass $${M_1} = 20\,kg$$ and $${M_2} = 12\,kg$$ are connected by a metal rod of mass $$8\,kg.$$ The system is pulled vertically up by applying a force of $$480\,N$$ as shown. The tension at the mid-point of the rod is :

A
$$144\,N$$
B
$$96\,N$$
C
$$240\,N$$
D
$$192\,N$$
Answer :
$$192\,N$$
34. Two forces are such that the sum of their magnitudes is $$18N$$ and their resultant is $$12N$$ which is perpendicular to the smaller force. Then the magnitudes of the forces are
A
$$12N,\,6N$$
B
$$13N,\,5N$$
C
$$10N,\,8N$$
D
$$16N,\,2N$$
Answer :
$$13N,\,5N$$
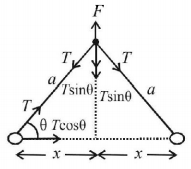
35. Two particles of mass $$m$$ each are tied at the ends of a light string of length $$2a.$$ The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance $$'a'$$ from the centre $$P$$ (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force $$F.$$ As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes $$2x,$$ is
A
$$\frac{F}{{2m}}\frac{a}{{\sqrt {{a^2} - {x^2}} }}$$
B
$$\frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}$$
C
$$\frac{F}{{2m}}\frac{x}{a}$$
D
$$\frac{F}{{2m}}\frac{{\sqrt {{a^2} - {x^2}} }}{x}$$
Answer :
$$\frac{F}{{2m}}\frac{x}{{\sqrt {{a^2} - {x^2}} }}$$
36. A marble block of mass $$2kg$$ lying on ice when given a velocity of $$6m/s$$ is stopped by friction in $$10s.$$ Then the coefficient of friction is
A
0.02
B
0.03
C
0.04
D
0.06
Answer :
0.06
37. A body, under the action of a force $$F = 6\hat i - 8\hat j + 10\hat k,$$ acquires an acceleration of $$1\,m{s^{ - 2}}.$$ The mass of this body must be
A
$$2\sqrt {10} \,kg$$
B
$$10\,kg$$
C
$$20\,kg$$
D
$$10\sqrt 2 \,kg$$
Answer :
$$10\sqrt 2 \,kg$$
38.
One end of a massless rope, which passes over a massless and frictionless pulley $$P$$ is tied to a hook $$C$$ while the other end is free. Maximum tension that the rope can bear is $$360\,N.$$ With what value of maximum safe acceleration $$\left( {{\text{in}}\,m{s^{ - 2}}} \right)$$ can a man of $$60\,kg$$ climb on the rope?

A
16
B
6
C
4
D
8
Answer :
4
39.
A system shown in the figure. Assume that cylinder remains in contact with the wedge and block hence the velocity of cylinder is

A
$$\frac{{\sqrt {19 - 4\sqrt 3 } }}{2}m/s$$
B
$$\frac{{\sqrt {13} }}{2}\,m/s$$
C
$$\sqrt 3 \,m/s$$
D
$$\sqrt 7 \,m/s$$
Answer :
$$\sqrt 7 \,m/s$$
40.
Two blocks $$A$$ and $$B$$ of masses $$3\,m$$ and $$m$$ respectively are connected by a massless and inextensible string. The whole inextensible string. The whole massless spring as shown in figure.
The magnitudes of acceleration of $$A$$ and $$B$$ immediately after the string is cut, are respectively :

A
$$\frac{g}{3},g$$
B
$$g,g$$
C
$$\frac{g}{3},\frac{g}{3}$$
D
$$g,\frac{g}{3}$$
Answer :
$$\frac{g}{3},g$$