21. If a stone is thrown out of an accelerated train, then acceleration of the stone at any instant depends on
A
force acting on it at that instant
B
acceleration of the train
C
Both (A) & (B)
D
None of these
Answer :
force acting on it at that instant
22. A pail filled with sand has a total mass of $$60\,kg.$$ A crane is lowering it such that it has an initial downward acceleration of $$1.5\,m/{s^2}.$$ A hole in the pail allows sand to leak out. If the force exerted by the crane on the pail does not change, what mass of sand must leak out before the downward acceleration decreases to zero?
A
$$9.2\,kg$$
B
$$20\,kg$$
C
$$40\,kg$$
D
$$51\,kg$$
Answer :
$$9.2\,kg$$
23.
A horizontal force of $$10N$$ is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. The weight of the block is

A
$$20N$$
B
$$50N$$
C
$$100N$$
D
$$2N$$
Answer :
$$2N$$
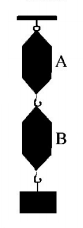
24.
A block of mass $$4\,kg$$ is suspended through two light spring balances $$A$$ and $$B.$$ Then $$A$$ and $$B$$ will read respectively :
A
$$4\,kg$$ and zero $$kg$$
B
zero $$kg$$ and $$4\,kg$$
C
$$4\,kg$$ and $$4\,kg$$
D
$$2\,kg$$ and $$2\,kg$$
Answer :
$$4\,kg$$ and $$4\,kg$$
25.
Two masses $${m_1} = 5kg$$ and $${m_2} = 4.8kg$$ tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move ?
$$\left( {g = 9.8m/{s^2}} \right)$$

A
$$5m/{s^2}$$
B
$$9.8m/{s^2}$$
C
$$0.2m/{s^2}$$
D
$$4.8m/{s^2}$$
Answer :
$$0.2m/{s^2}$$
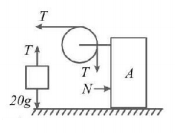
26.
The elevator shown in fig. is descending with an acceleration of $$2\,m/{s^2}.$$ The mass of the block $$A = 0.5\,kg.$$ The force exerted by the block $$A$$ on block $$B$$ is

A
$$2\,N$$
B
$$4\,N$$
C
$$6\,N$$
D
$$8\,N$$
Answer :
$$4\,N$$
27. A horizontal uniform rope of length $$L,$$ resting on a frictionless horizontal surface, is pulled at one end by force $$F.$$ What is the tension in the rope at a distance $$l$$ from the end where the force is applied?
A
$$F\left( {1 - \frac{l}{L}} \right)$$
B
$$2F\left( {1 - \frac{l}{{2L}}} \right)$$
C
$$\frac{F}{L}$$
D
$$\frac{F}{l}\left( {1 - \frac{l}{L}} \right)$$
Answer :
$$F\left( {1 - \frac{l}{L}} \right)$$
28.
A block is kept on a frictionless inclined surface with angle of inclination $$'\alpha '.$$ The incline is given an acceleration $$'a'$$ to keep the block stationary. Then $$a$$ is equal to

A
$$g\,{\text{cosec}}\,\alpha $$
B
$$\frac{g}{{\tan \alpha }}$$
C
$$g\tan \alpha $$
D
$$g$$
Answer :
$$g\tan \alpha $$
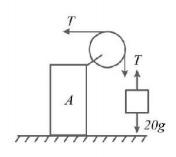
29.
A $$20\,kg$$ block $$B$$ is suspended from a cord attached to a $$40\,kg$$ cart $$A.$$ Find the ratio of the acceleration of block in cases (i) and (ii) shown in the figure immediately after the system is released from rest. (neglect friction)

A
$$\frac{{\sqrt 2 }}{3}$$
B
$$3\sqrt 2 $$
C
$$\frac{3}{2}$$
D
$$\frac{3}{{2\sqrt 2 }}$$
Answer :
$$\frac{3}{{2\sqrt 2 }}$$
30.
Two monkeys of masses $$10\,kg$$ and $$8\,kg$$ are moving along a vertical rope which is light and inextensible, the former climbing up with an acceleration of $$2\,m/{s^2}$$ while the latter coming down with a uniform velocity of $$2\,m/s.$$ Find the tension (in newtons).

A
$$200\,N$$
B
$$150\,N$$
C
$$300\,N$$
D
$$100\,N$$
Answer :
$$200\,N$$