91. A light string passing over a smooth light pulley connects two blocks of masses $${m_1}$$ and $${m_2}$$ (vertically). If the acceleration of the system is $$\frac{g}{8},$$ then the ratio of the masses is
A
$$8:1$$
B
$$9:7$$
C
$$4:3$$
D
$$5:3$$
Answer :
$$9:7$$
92.
Given in the figure are two blocks $$A$$ and $$B$$ of weight $$20N$$ and $$100N,$$ respectively. These are being pressed against a wall by a force $$F$$ as shown. If the coefficient of friction between the blocks is 0.1 and between block $$B$$ and the wall is 0.15, the frictional force applied by the wall on block $$B$$ is:

A
$$120\,N$$
B
$$150\,N$$
C
$$100\,N$$
D
$$80\,N$$
Answer :
$$120\,N$$
93.
Consider a car moving on a straight road with a speed of $$100m/s .$$ The distance at which car can be stopped is
$$\left[ {{\mu _k} = 0.5} \right]$$
A
$$1000m$$
B
$$800m$$
C
$$400m$$
D
$$100m$$
Answer :
$$1000m$$
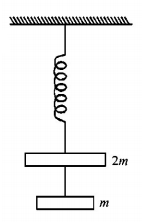
94.
The string between blocks of mass $$m$$ and $$2m$$ is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass $$2m$$ and $$m$$ (immediately after cutting)
A
g, g
B
$$g,\frac{g}{2}$$
C
$$\frac{g}{2},g$$
D
$$\frac{g}{2},\frac{g}{2}$$
Answer :
$$\frac{g}{2},g$$
95.
Two blocks $${m_1} = 5\,gm$$ and $${m_2} = 10\,gm$$ are hung vertically over a light frictionless pulley as shown here. What is the acceleration of the masses when they are left free?

A
$$\frac{g}{3}$$
B
$$\frac{g}{2}$$
C
$$g$$
D
$$\frac{g}{5}$$
Answer :
$$\frac{g}{3}$$
96. A triangular block of mass $$M$$ with angles $${30^ \circ },{60^ \circ },$$ and $${90^ \circ }$$ rests with its $${30^ \circ } - {90^ \circ }$$ side on a horizontal table. A cubical block of mass $$m$$ rests on the $${60^ \circ } - {30^ \circ }$$ side. The acceleration which $$M$$ must have relative to the table to keep $$m$$ stationary relative to the triangular block assuming frictionless contact is
A
$$g$$
B
$$\frac{g}{{\sqrt 2 }}$$
C
$$\frac{g}{{\sqrt 3 }}$$
D
$$\frac{g}{{\sqrt 5 }}$$
Answer :
$$\frac{g}{{\sqrt 3 }}$$




