311.
Three elephants $$A,B$$ and $$C$$ are moving along a straight line with constant speed in same direction as shown in figure. Speed of $$A$$ is $$5\,m/s$$ and speed of $$C$$ is $$10\,m/s.$$ Initially separation between $$A$$ and $$B$$ is $$'d'$$ and between $$B$$ and $$C$$ is also $$d.$$ When $$'B'$$ catches $$'C'$$ separation between $$A$$ and $$C$$ becomes $$3d.$$ Then the speed of $$B$$ will be

A
$$7.5\,m/s$$
B
$$15\,m/s$$
C
$$20\,m/s$$
D
$$5\,m/s$$
Answer :
$$15\,m/s$$
312. A particle moves along a circle of radius $$\left( {\frac{{20}}{\pi }} \right)m$$ with constant tangential acceleration. If the velocity of the particle is $$80\,m/s$$ at the end of the second revolution after motion has begin, the tangential acceleration is
A
$$160\,\pi \,m/{s^2}$$
B
$$40\,m/{s^2}$$
C
$$40\,\pi \,m/{s^2}$$
D
$$640\,\pi \,m/{s^2}$$
Answer :
$$40\,m/{s^2}$$
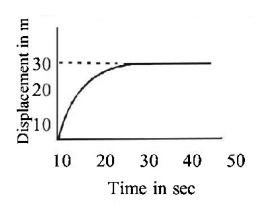
313.
The displacement of a particle as a function of time is shown in figure. It indicates that
A
the velocity of the particle is constant throughout
B
the acceleration of the particle is constant throughout
C
the particle starts with a constant velocity and is accelerated
D
the motion is retarded and finally the particle stops
Answer :
the motion is retarded and finally the particle stops
314. If the vectors $$\left( {\hat i + \hat j + \hat k} \right)$$ and $$3\hat i$$ form two sides of a triangle, the area of the triangle is :
A
$$\sqrt 3 $$
B
$$2\sqrt 3 $$
C
$$\frac{3}{{\sqrt 2 }}$$
D
$$3\sqrt 2 $$
Answer :
$$\frac{3}{{\sqrt 2 }}$$
315. A projectile is thrown at an angle of $${40^ \circ }$$ with the horizontal and its range is $${R_1}.$$ Another projectile is thrown at an angle $${40^ \circ }$$ with the vertical and its range is $${R_2}.$$ What is the relation between $${R_1}$$ and $${R_2}$$ ?
A
$${R_1} = {R_2}$$
B
$${R_1} = 2{R_2}$$
C
$$2{R_1} = {R_2}$$
D
$${R_1} = \frac{{4{R_2}}}{5}$$
Answer :
$${R_1} = {R_2}$$
316. An automobile travelling with a speed of $$60 \,km/h,$$ can brake to stop within a distance of $$20 \,m.$$ If the car is going twice as fast i.e., $$120 \,km/h,$$ the stopping distance will be-
A
$$60 \,m$$
B
$$40 \,m$$
C
$$20 \,m$$
D
$$80 \,m$$
Answer :
$$80 \,m$$
317. The displacement-time graphs of two particles $$A$$ and $$B$$ are straight lines making angles of $${30^ \circ }$$ and $${60^ \circ }$$ respectively with the time axis. If the velocity of $$A$$ is $${v_A}$$ and that of $$B$$ is $${v_B},$$ the value of $$\frac{{{v_A}}}{{{v_B}}}$$ is
A
$$\frac{1}{2}$$
B
$$\frac{1}{{\sqrt 3 }}$$
C
$$\sqrt 3 $$
D
$$\frac{1}{3}$$
Answer :
$$\frac{1}{3}$$
318. An object, moving with a speed of $$6.25\,m/s,$$ is decelerated at a rate given by: $$\frac{{dv}}{{dt}} = - 2.5\sqrt v $$ where $$v$$ is the instantaneous speed. The time taken by the object, to come to rest, would be
A
$$2\,s$$
B
$$4\,s$$
C
$$8\,s$$
D
$$1\,s$$
Answer :
$$2\,s$$
319. Two cars $$P$$ and $$Q$$ start from a point at the same time in a straight line and their positions are represented by $${X_P}\left( t \right) = at + b{t^2}$$ and $${X_Q}\left( t \right) = ft - {t^2}.$$ At what time do the cars have the same velocity?
A
$$\frac{{a - f}}{{1 + b}}$$
B
$$\frac{{a + f}}{{2\left( {b - 1} \right)}}$$
C
$$\frac{{a + f}}{{2\left( {1 + b} \right)}}$$
D
$$\frac{{f - a}}{{2\left( {1 + b} \right)}}$$
Answer :
$$\frac{{f - a}}{{2\left( {1 + b} \right)}}$$
320. Two trains are each $$50\,m$$ long moving parallel towards each other at speeds $$10\,m/s$$ and $$15\,m/s$$ respectively. After what time will they pass each other?
A
$$5\sqrt {\frac{2}{3}} \sec $$
B
$$4\,\sec $$
C
$$2\,\sec $$
D
$$6\,\sec $$
Answer :
$$4\,\sec $$