281. A body is thrown vertically upwards from the ground. It reaches a maximum height of $$20\,m$$ in $$5\,s.$$ After what time it will reach the ground from its maximum height position?
A
$$2.5\,s$$
B
$$5\,s$$
C
$$10\,s$$
D
$$25\,s$$
Answer :
$$5\,s$$
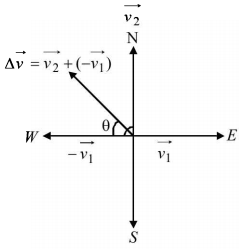
282. A particle is moving eastwards with a velocity of $$5\,m{s^{ - 1}}.$$ In $$10$$ seconds the velocity changes to $$5\,m{s^{ - 1}}$$ northwards. The average acceleration in this time is-
A
$$\frac{1}{2}\,m{s^{ - 2}}$$ towards north
B
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-east
C
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-west
D
Zero
Answer :
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-west
283. A person moves $$30\,m$$ north and then $$20\,m$$ towards east and finally $$30\sqrt 2 \,m$$ in south-west direction. The displacement of the person from the origin will be
A
$$10\,m$$ along north
B
$$10\,m$$ along south
C
$$10\,m$$ along west
D
zero
Answer :
$$10\,m$$ along west
284. A stone is dropped from a rising balloon at a height of $$76\,m$$ above the ground and reaches the ground in $$6s.$$ What was the velocity of the balloon when the stone was dropped? Take $$g = 10\,m/{s^2}.$$
A
$$\left( {\frac{{52}}{3}} \right)\,m/s\,{\text{upward}}$$
B
$$\left( {\frac{{52}}{3}} \right)\,m/s\,{\text{downward}}$$
C
$$3\,m/s$$
D
$$9.8\,m/s$$
Answer :
$$\left( {\frac{{52}}{3}} \right)\,m/s\,{\text{upward}}$$
285.
A body starts from rest at time $$t = 0,$$ the acceleration time graph is shown in the figure. The maximum velocity attained by the body will be-

A
$$110 \,m/s$$
B
$$55 \,m/s$$
C
$$650 \,m/s$$
D
$$550 \,m/s$$
Answer :
$$55 \,m/s$$
286. A projectile is thrown in the upward direction making an angle of $${60^ \circ }$$ with the horizontal direction with a velocity of $$147\,m{s^{ - 1}}.$$ Then the time after which its inclination with the horizontal is $${45^ \circ },$$ is
A
$$15\,s$$
B
$$10.98\,s$$
C
$$5.49\,s$$
D
$$2.745\,s$$
Answer :
$$5.49\,s$$
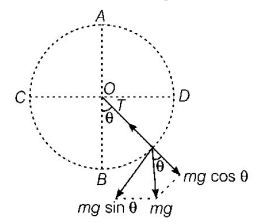
287.
A stone is attached to one end of a string and rotated in a vertical circle. If string breaks at the position of maximum tension, it will break at

A
$$A$$
B
$$B$$
C
$$C$$
D
$$D$$
Answer :
$$B$$
288. Vector $$\overrightarrow A $$ makes equal angle with $$x,y$$ and $$z$$-axis. Value of its components in terms of magnitude of $$\overrightarrow A $$ will be
A
$$\frac{A}{{\sqrt 3 }}$$
B
$$\frac{A}{{\sqrt 2 }}$$
C
$$\sqrt 3 A$$
D
$$\frac{{\sqrt 3 }}{A}$$
Answer :
$$\frac{A}{{\sqrt 3 }}$$
289. A ball is thrown vertically up (taken as $$+ z$$ -axis) from the ground. The correct momentum-height ($$p-h$$ ) diagram is:
A


B


C


D


Answer :


290. A particle is moving with velocity $$\vec v = k\left( {y\,\hat i + x\,\hat j} \right),$$ where $$k$$ is a constant. The general equation for its path is-
A
$$y = {x^2} + {\text{ constant}}$$
B
$${y^2} = x + {\text{ constant}}$$
C
$$xy = {\text{ constant}}$$
D
$${y^2} = {x^2} + {\text{ constant}}$$
Answer :
$${y^2} = {x^2} + {\text{ constant}}$$