Question

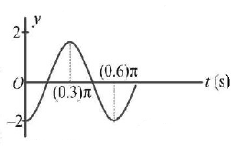
Part of a simple harmonic motion is graphed in the figure, where $$y$$ is the displacement from the mean position. The correct equation describing this $$S.H.M.$$  is
Simple Harmonic Motion (SHM) mcq question image

A. $$y = 4\cos \left( {0.6t} \right)$$
B. $$y = 2\sin \left( {\frac{{10}}{3}t - \frac{\pi }{2}} \right)$$  
C. $$y = 4\sin \left( {\frac{{10}}{3}t + \frac{\pi }{2}} \right)$$
D. $$y = 2\cos \left( {\frac{{10}}{3}t + \frac{\pi }{2}} \right)$$
Answer :   $$y = 2\sin \left( {\frac{{10}}{3}t - \frac{\pi }{2}} \right)$$
Solution :
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{figure,}}\,\,\frac{T}{2} = 0.3\pi , \cr & \therefore T = 0.6\,\pi \,\,{\text{and}}\,\,{\phi _0} = - \frac{\pi }{2}. \cr & {\text{Thus}}\,\,y = A\sin \left( {\omega t + {\phi _0}} \right) = 2\sin \left\{ {\frac{{2\pi }}{{0.6\pi }}t + \left( { - \frac{\pi }{2}} \right)} \right\} \cr & = 2\sin \left( {\frac{{10t}}{3} - \frac{\pi }{2}} \right). \cr} $$

Releted MCQ Question on
Oscillation and Mechanical Waves >> Simple Harmonic Motion (SHM)

Releted Question 1

Two bodies $$M$$ and $$N$$ of equal masses are suspended from two separate massless springs of spring constants $${k_1}$$ and $${k_2}$$ respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of $$M$$ to that of $$N$$ is

A. $$\frac{{{k_1}}}{{{k_2}}}$$
B. $$\sqrt {\frac{{{k_1}}}{{{k_2}}}} $$
C. $$\frac{{{k_2}}}{{{k_1}}}$$
D. $$\sqrt {\frac{{{k_2}}}{{{k_1}}}} $$
View Answer
Releted Question 2

A particle free to move along the $$x$$-axis has potential energy given by $$U\left( x \right) = k\left[ {1 - \exp \left( { - {x^2}} \right)} \right]$$      for $$ - \infty \leqslant x \leqslant + \infty ,$$    where $$k$$ is a positive constant of appropriate dimensions. Then

A. at points away from the origin, the particle is in unstable equilibrium
B. for any finite nonzero value of $$x,$$ there is a force directed away from the origin
C. if its total mechanical energy is $$\frac{k}{2},$$  it has its minimum kinetic energy at the origin.
D. for small displacements from $$x = 0,$$  the motion is simple harmonic
View Answer
Releted Question 3

The period of oscillation of a simple pendulum of length $$L$$ suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination $$\alpha ,$$ is given by

A. $$2\pi \sqrt {\frac{L}{{g\cos \alpha }}} $$
B. $$2\pi \sqrt {\frac{L}{{g\sin \alpha }}} $$
C. $$2\pi \sqrt {\frac{L}{g}} $$
D. $$2\pi \sqrt {\frac{L}{{g\tan \alpha }}} $$
View Answer
Releted Question 4

A particle executes simple harmonic motion between $$x = - A$$  and $$x = + A.$$  The time taken for it to go from 0 to $$\frac{A}{2}$$ is $${T_1}$$ and to go from $$\frac{A}{2}$$ to $$A$$ is $${T_2.}$$ Then

A. $${T_1} < {T_2}$$
B. $${T_1} > {T_2}$$
C. $${T_1} = {T_2}$$
D. $${T_1} = 2{T_2}$$
View Answer

Practice More Releted MCQ Question on
Simple Harmonic Motion (SHM)

Practice More MCQ Question on Physics Section

Basic PhysicsUnit and MeasurementKinematicsLaws of MotionFrictionUniform Circular MotionImpulseMomentumWork Energy and PowerRotational MotionGravitationMechanical Properties of Solids and Fluids
Heat and ThermodynamicsThermodynamicsThermal ExpansionConductionRadiationCalorimetryKinetic Theory of Gases
Electrostatics and MagnetismElectric ChargesElectric FieldElectric PotentialCapacitors and DielectricsMagnetic Effect of CurrentMagnetic MaterialsElectromagnetic WavesElectric CurrentElectromagnetic InductionAlternating CurrentSemiconductors and Electronic Devices
Optics and WaveRay OpticsWave Optics
Modern PhysicsDual Nature of Matter and RadiationAtoms And NucleiAtoms or Nuclear Fission and FusionRadioactivityModern Physics MiscellaneousSemiconductors and Electronic Devices
Oscillation and Mechanical WavesSimple Harmonic Motion (SHM)Waves