Question
On interchanging the resistances, the balance point of a meter bridge shifts to the left by $$10\,cm.$$ The resistance of their series combination is $$1k\,\Omega $$. How much was the resistance on the left slot before interchanging the resistances?
A.
$$990\,\Omega $$
B.
$$505\,\Omega $$
C.
$$550\,\Omega $$
D.
$$910\,\Omega $$
Answer :
$$550\,\Omega $$
Solution :
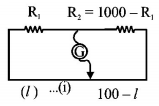
$$\eqalign{ & {R_1} + {R_2} = 1000 \cr & \Rightarrow {R_2} = 1000 - {R_1} \cr} $$
On balancing condition
$${R_1}\left( {100 - l} \right) = \left( {1000 - {R_1}} \right)l\,......\left( {\text{i}} \right)$$
On Interchanging resistance balance point shifts left by $$10\,cm$$
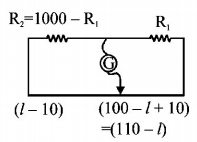
On balancing condition
$$\eqalign{ & \left( {1000 - {R_1}} \right)\left( {110 - l} \right) = {R_1}\left( {l - 10} \right) \cr & {\text{or,}}\,{R_1}\left( {l - 10} \right) = \left( {1000 - {R_1}} \right)\left( {110 - l} \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Dividing eqn (i) by (ii)
$$\eqalign{ & \frac{{100 - l}}{{l - 10}} = \frac{l}{{110 - l}} \cr & \Rightarrow \left( {100 - l} \right)\left( {110 - l} \right) = l\left( {l - 10} \right) \cr & \Rightarrow 11000 - 100l - 110l + {l^2} = {l^2} - 10l \cr & \Rightarrow 11000 = 200l \cr & {\text{or,}}\,l = 55 \cr} $$
Putting the value of $$'l'$$ in eqn (i)
$$\eqalign{ & {R_1}\left( {100 - 55} \right) = \left( {1000 - {R_1}} \right)55 \cr & \Rightarrow {R_1}\left( {45} \right) = \left( {1000 - {R_1}} \right)55 \cr & \Rightarrow {R_1}\left( 9 \right) = \left( {1000 - {R_1}} \right)11 \cr & \Rightarrow 20{R_1} = 11000 \cr & \therefore {R_1} = 550K\Omega \cr} $$
$$\eqalign{ & {R_1} + {R_2} = 1000 \cr & \Rightarrow {R_2} = 1000 - {R_1} \cr} $$
On balancing condition
$${R_1}\left( {100 - l} \right) = \left( {1000 - {R_1}} \right)l\,......\left( {\text{i}} \right)$$

On Interchanging resistance balance point shifts left by $$10\,cm$$

On balancing condition
$$\eqalign{ & \left( {1000 - {R_1}} \right)\left( {110 - l} \right) = {R_1}\left( {l - 10} \right) \cr & {\text{or,}}\,{R_1}\left( {l - 10} \right) = \left( {1000 - {R_1}} \right)\left( {110 - l} \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Dividing eqn (i) by (ii)
$$\eqalign{ & \frac{{100 - l}}{{l - 10}} = \frac{l}{{110 - l}} \cr & \Rightarrow \left( {100 - l} \right)\left( {110 - l} \right) = l\left( {l - 10} \right) \cr & \Rightarrow 11000 - 100l - 110l + {l^2} = {l^2} - 10l \cr & \Rightarrow 11000 = 200l \cr & {\text{or,}}\,l = 55 \cr} $$
Putting the value of $$'l'$$ in eqn (i)
$$\eqalign{ & {R_1}\left( {100 - 55} \right) = \left( {1000 - {R_1}} \right)55 \cr & \Rightarrow {R_1}\left( {45} \right) = \left( {1000 - {R_1}} \right)55 \cr & \Rightarrow {R_1}\left( 9 \right) = \left( {1000 - {R_1}} \right)11 \cr & \Rightarrow 20{R_1} = 11000 \cr & \therefore {R_1} = 550K\Omega \cr} $$
