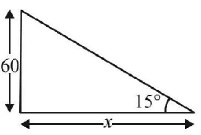
81. From the top of a light-house 60 metres high with its base at the sea-level, the angle of depression of a boat is 15°. The distance of the boat from the foot of the light house is
A
$$\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}} \right)60\,{\text{metres}}$$
B
$$\left( {\frac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}}} \right)60\,{\text{metres}}$$
C
$${\left( {\frac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}}} \right)^2}{\text{metres}}$$
D
none of these
Answer :
$$\left( {\frac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}}} \right)60\,{\text{metres}}$$
82. If in the $$\vartriangle ABC,$$ the incentre is the middle point of the median $$AD$$ then $$\cos A$$ has the value
A
$$\frac{7}{8}$$
B
$$\frac{1}{4}$$
C
$$\frac{1}{3}$$
D
$$\frac{1}{{\sqrt 2 }}$$
Answer :
$$\frac{1}{4}$$
83. The ratio of the distances of the orthocentre of an acute-angled $$\vartriangle ABC$$ from the sides $$BC, AC$$ and $$AB$$ is
A
$$\cos A:\cos B:\cos C$$
B
$$\sin A:\sin B:\sin C$$
C
$$\sec A:\sec B:\sec C$$
D
None of these
Answer :
$$\sec A:\sec B:\sec C$$
84. If in a $$\vartriangle ABC,c\,{\cos ^2}\frac{A}{2} + a\,{\cos ^2}\frac{C}{2} = \frac{{3b}}{2},$$ then $$a,b,c$$ are in
A
G.P.
B
H.P.
C
A.P.
D
None of these
Answer :
A.P.
85. The angle of elevation of the top of a tower from two places situated at distances $$21\,m.$$ and $$x\,m.$$ from the base of the tower are $${45^ \circ }$$ and $${60^ \circ }$$ respectively. What is the value of $$x\,?$$
A
$$7\sqrt 3 $$
B
$$7 - \sqrt 3 $$
C
$$7 + \sqrt 3 $$
D
$$14$$
Answer :
$$7\sqrt 3 $$
86. If in a $$\Delta \,ABC\,\,a\,{\cos ^2}\left( {\frac{C}{2}} \right) + c\,{\cos ^2}\left( {\frac{A}{2}} \right) = \frac{{3b}}{2},$$ then the sides $$a, b$$ and $$c$$
A
satisfy $$a + b = c$$
B
are in A.P.
C
are in G.P.
D
are in H.P.
Answer :
are in A.P.
87. If the bisector of the angle $$P$$ of a triangle $$PQR$$ meets $$QR$$ in $$S,$$ then
A
$$QS = SR$$
B
$$QS : SR = PR : PQ$$
C
$$QS : SR = PQ : PR$$
D
None of these
Answer :
$$QS : SR = PQ : PR$$
88. Given that $$a, b, c$$ are the sides of a triangle $$ABC$$ which is right angled at $$C,$$ then the minimum value of $${\left( {\frac{c}{a} + \frac{c}{b}} \right)^2}$$ is
A
0
B
4
C
6
D
8
Answer :
8
89. The area of a $$\vartriangle ABC$$ is $${a^2} - {\left( {b - c} \right)^2}.$$ Then $$\tan A$$ is equal to
A
$$\frac{4}{3}$$
B
$$\frac{3}{4}$$
C
$$\frac{8}{15}$$
D
None of these
Answer :
$$\frac{8}{15}$$
90. Each side of an equilateral triangle subtends an angle of $${60^ \circ }$$ at the top of a tower $$h\, m$$ high located at the centre of the triangle. If $$a$$ is the length of each of side of the triangle, then
A
$$3{a^2} = 2{h^2}$$
B
$$2{a^2} = 3{h^2}$$
C
$${a^2} = 3{h^2}$$
D
$$3{a^2} = {h^2}$$
Answer :
$$2{a^2} = 3{h^2}$$