71.
In a triangle with sides $$a, b, c,$$ $${r_1} > {r_2} > {r_3}$$ (which are the ex-radii) then A
$$a > b > c$$
B
$$a < b < c$$
C
$$a > b$$ and $$b < c$$
D
$$a < b$$ and $$b > c$$
Answer :
$$a > b > c$$
View Solution
Discuss Question
$$\eqalign{
& {r_1} > {r_2} > {r_3} \cr
& \Rightarrow \,\,\frac{\Delta }{{s - a}} > \frac{\Delta }{{s - b}} > \frac{\Delta }{{s - c}}; \cr
& \Rightarrow \,\,s - a < s - b < s - c \cr
& \Rightarrow \,\, - a < - b < - c \cr
& \Rightarrow \,\,a > b > c \cr} $$
72.
The length of the shadow of a pole inclined at $${10^ \circ }$$ to the vertical towards the sun is 2.05 metres, when the elevation of the sun is $${38^ \circ }.$$ The length of the pole is A
$$\frac{{2.05\sin {{38}^ \circ }}}{{\sin {{42}^ \circ }}}$$
B
$$\frac{{2.05\sin {{42}^ \circ }}}{{\sin {{38}^ \circ }}}$$
C
$$\frac{{2.05\cos {{38}^ \circ }}}{{\cos {{42}^ \circ }}}$$
D
None of these
Answer :
$$\frac{{2.05\sin {{38}^ \circ }}}{{\sin {{42}^ \circ }}}$$
View Solution
Discuss Question
$$\eqalign{
& \frac{{\sin {{38}^ \circ }}}{l} = \frac{{\sin \left( {SPO} \right)}}{{2.05}} \cr
& = \frac{{\sin \left( {{{180}^ \circ } - {{38}^ \circ } - {{90}^ \circ } - {{10}^ \circ }} \right)}}{{2.05}} \cr
& \Rightarrow l = \frac{{2.05\sin {{38}^ \circ }}}{{\sin {{42}^ \circ }}} \cr} $$
73.
If the sides of a triangle are in G.P. and the largest angle is twice the smallest angle then the common ratio, which is greater than 1, lies in the interval A
$$\left( {1,\sqrt 3 } \right)$$
B
$$\left( {1,\root 4 \of 3 } \right)$$
C
$$\left( {1,\frac{{\sqrt 5 + 1}}{2}} \right)$$
D
None of these
Answer :
$$\left( {1,\root 4 \of 3 } \right)$$
View Solution
Discuss Question
$$b = ar,c = a{r^2},$$ where $$r > 1.$$
74.
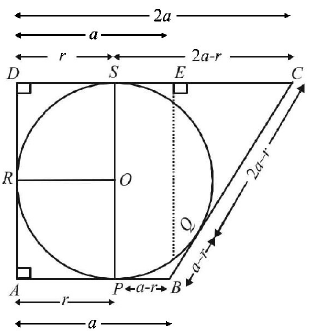
Let $$ABCD$$ be a quadrilateral with area 18, with side $$AB$$ parallel to the side $$CD$$ and $$2AB = CD.$$ Let $$AD$$ be perpendicular to $$AB$$ and $$CD.$$ If a circle is drawn inside the quadrilateral $$ABCD$$ touching all the sides, then its radius is A
3
B
2
C
$$\frac{3}{2}$$
D
1
Answer :
2
View Solution
Discuss Question
$${\text{Given }}AB\parallel CD,$$ $$CD = 2AB$$
Let $$AB = a$$ then $$CD = 2a$$ Let radius of circle be $$r.$$ Let circle touches $$AB$$ at $$P, BC$$ at $$Q, AD$$ at $$R$$ and $$CD$$ at $$S.$$
Then $$AR = AP = r, BP = BQ = a - r$$
$$DR = DS = r$$ and $$CQ = CS = 2a - r$$ In $$\Delta BEC$$
$$\eqalign{
& B{C^2} = B{E^2} + E{C^2} \cr
& \Rightarrow \,\,{\left( {a - r + 2a - r} \right)^2} = {\left( {2r} \right)^2} + {\left( a \right)^2} \cr
& \Rightarrow \,\,9{a^2} + 4{r^2} - 12ar = 4{r^2} + {a^2} \cr
& \Rightarrow \,\,a = \frac{3}{2}r\,\,\,\,\,\,\,.....\left( 1 \right) \cr} $$
Also $$Ar$$ (quad. $$ABCD$$ ) $$=$$ 18
$$\eqalign{
& \Rightarrow \,\,a \times 2r + \frac{1}{2} \times a \times 2r = 18 \cr
& \Rightarrow \,\,ar = 6 \cr
& \Rightarrow \,\,\frac{{3{r^2}}}{2} = 6\,\left( {{\text{using equation }}\left( 1 \right)} \right) \cr
& \Rightarrow \,\,{r^2} = 4 \cr
& \Rightarrow \,\,r = 2 \cr} $$
75.
If in a $$\vartriangle ABC,AC = 12,BC = 13$$ and $$AB = 5,$$ then the distance of $$A$$ from $$BC$$ is A
$$\frac{{25}}{{13}}$$
B
$$\frac{{60}}{{13}}$$
C
$$\frac{{65}}{{12}}$$
D
None of these
Answer :
$$\frac{{60}}{{13}}$$
View Solution
Discuss Question
$$\frac{1}{2} \cdot p \cdot a = {\text{area}} = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} .$$
76.
The base of a cliff is circular. From the extremities of a diameter of the base the angles of elevation of the top of the cliff are $${30^ \circ }$$ and $${60^ \circ }.$$ If the height of the cliff be 500 metres, then the diameter of the base of the cliff is A
$$1000\sqrt 3 \,m$$
B
$$\frac{{2000}}{{\sqrt 3 }}m$$
C
$$\frac{{1000}}{{\sqrt 3 }}m$$
D
$$2000\sqrt 2 \,m$$
Answer :
$$\frac{{2000}}{{\sqrt 3 }}m$$
View Solution
Discuss Question
$$\eqalign{
& {d_2} = h\cot {30^ \circ } = 500\sqrt 3 , \cr
& {\text{and }}{d_1} = \frac{{500}}{{\sqrt 3 }} \cr} $$
$${\text{Diameter }}d = 500\sqrt 3 + \frac{{500}}{3}\sqrt 3 = \frac{{2000}}{{\sqrt 3 }}m$$
77.
In a $$\vartriangle ABC,$$ the tangent of half the difference of two angles is one-third the tangent of half the sum of the two angles. The ratio of the sides opposite the angles is A
2 : 3
B
1 : 3
C
1 : 2
D
3 : 4
Answer :
1 : 2
View Solution
Discuss Question
$$\eqalign{
& \tan\frac{{A - B}}{2} = \frac{1}{3}\tan \frac{{A + B}}{2} = \frac{1}{3}\cot \frac{C}{2} \cr
& \Rightarrow \,\,\frac{{a - b}}{{a + b}} = \frac{1}{3}. \cr} $$
78.
In a $$\vartriangle ABC,\tan \frac{A}{2}$$ and $$\tan \frac{B}{2}$$ satisfy $$6{x^2} - 5x + 1 = 0.$$ Then A
$${a^2} + {b^2} > {c^2}$$
B
$${a^2} - {b^2} = {c^2}$$
C
$${a^2} + {b^2} = {c^2}$$
D
None of these
Answer :
$${a^2} + {b^2} = {c^2}$$
View Solution
Discuss Question
$$\eqalign{
& \tan \frac{A}{2} + \tan \frac{B}{2} = \frac{5}{6},\tan \frac{A}{2} \cdot \tan \frac{B}{2} = \frac{1}{6} \cr
& \Rightarrow \,\,\tan \left( {\frac{{A + B}}{2}} \right) = 1 \cr
& \Rightarrow \,\,A + B = 2 \times \frac{\pi }{4}. \cr} $$
79.
The upper part of a tree broken over by the wind makes an angle of $${30^ \circ }$$ with the ground and the distance from the root to the point where the top of the tree touches the ground is $$10\,m;$$ what was the height of the tree A
$$8.66\,m$$
B
$$15\,m$$
C
$$17.32\,m$$
D
$$25.98\,m$$
Answer :
$$17.32\,m$$
View Solution
Discuss Question
Height of tree is
$$AB + AC = \frac{{20}}{{\sqrt 3 }} + \frac{{10}}{{\sqrt 3 }} = \frac{{30}}{{\sqrt 3 }} = 10\sqrt 3 = 17.32\,m$$
80.
The angles of a right-angled triangle are in A.P. The ratio of the inradius and the perimeter is A
$$\left( {2 - \sqrt 3 } \right):2\sqrt 3 $$
B
$$1:8\sqrt 3 \left( {2 + \sqrt 3 } \right)$$
C
$$\left( {2 + \sqrt 3 } \right):4\sqrt 3 $$
D
None of these
Answer :
$$\left( {2 - \sqrt 3 } \right):2\sqrt 3 $$
View Solution
Discuss Question
$$\left( {\alpha - \beta } \right) + \alpha + \left( {\alpha + \beta } \right) = {180^ \circ }\,\,{\text{and }}\alpha + \beta = {90^ \circ }.$$