51.
If in a $$\Delta \,ABC,$$ the altitudes from the vertices $$A, B, C$$ on opposite sides are in H.P, then $$\sin A, \sin B, \sin C$$ are in A
G.P.
B
A.P.
C
A.P. - G.P.
D
H.P.
Answer :
A.P.
View Solution
Discuss Question
$$\eqalign{
& \Delta = \frac{1}{2}{p_1}a = \frac{1}{2}{p_2}b = \frac{1}{2}{p_3}b \cr
& {p_1},{p_2},{p_3}\,\,{\text{are in H}}{\text{.P}}{\text{.}} \cr
& \Rightarrow \,\,\frac{{2\Delta }}{a},\frac{{2\Delta }}{b},\frac{{2\Delta }}{c}\,\,{\text{are in H}}{\text{.P}}{\text{.}} \cr
& \Rightarrow \,\,\frac{1}{a},\frac{1}{b},\frac{1}{c}\,\,{\text{are in H}}{\text{.P}}{\text{.}} \cr
& \Rightarrow \,\,a,b,c\,\,{\text{are in A}}{\text{.P}}{\text{.}} \cr} $$
52.
In a $$\vartriangle ABC,\frac{{c + b}}{{c - b}} \cdot \tan \frac{A}{2}$$ is equal to A
$$\tan \left( {\frac{A}{2} + B} \right)$$
B
$$\cot \left( {\frac{A}{2} + B} \right)$$
C
$$\tan \left( {A + \frac{B}{2}} \right)$$
D
None of these
Answer :
$$\tan \left( {\frac{A}{2} + B} \right)$$
View Solution
Discuss Question
$$\eqalign{
& \frac{{c + b}}{{c - b}}\tan \frac{A}{2} = \frac{{\sin C + \sin B}}{{\sin C - \sin B}}\tan \frac{A}{2} = \frac{{2\sin \frac{{B + C}}{2} \cdot \cos \frac{{C - B}}{2}}}{{2\cos \frac{{B + C}}{2} \cdot \sin \frac{{C - B}}{2}}} \cdot \tan \frac{A}{2} \cr
& \frac{{c + b}}{{c - b}}\tan \frac{A}{2} = \tan \frac{{B + C}}{2} \cdot \cot \frac{{C - B}}{2} \cdot \tan \frac{A}{2} = \cot \frac{{C - B}}{2} = \cot \frac{{\pi - A - B - B}}{2} \cr
& \frac{{c + b}}{{c - b}}\tan \frac{A}{2} = \cot\left( {\frac{\pi }{2} - \overline {\frac{A}{2} + B} } \right) = \tan \left( {\frac{A}{2} + B} \right). \cr} $$
53.
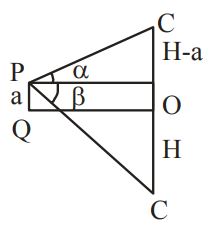
From a point a metre above a lake the angle of elevation of a cloud is $$\alpha $$ and the angle of depression of its reflection is $$\beta .$$ The height of the cloud is A
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\alpha - \beta } \right)}}{\text{metre}}$$
B
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}{\text{metre}}$$
C
$$\frac{{a\sin \left( {\alpha - \beta } \right)}}{{\sin \left( {\alpha + \beta } \right)}}{\text{metre}}$$
D
None of these
Answer :
$$\frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}{\text{metre}}$$
View Solution
Discuss Question
$$\left( {H + a} \right)\cot b = \left( {H - a} \right)\cot a$$
using componendo and dividendo
$$ \Rightarrow H = \frac{{a\sin \left( {\alpha + \beta } \right)}}{{\sin \left( {\beta - \alpha } \right)}}$$
54.
In a $$\vartriangle ABC,a = 1$$ and the perimeter is six times the AM of the sines of the angles. The measure of $$\angle A$$ is A
$$\frac{\pi }{3}$$
B
$$\frac{\pi }{2}$$
C
$$\frac{\pi }{6}$$
D
$$\frac{\pi }{4}$$
Answer :
$$\frac{\pi }{6}$$
View Solution
Discuss Question
$$\eqalign{
& 1 + b + c = 6.\frac{{\sin A + \sin B + \sin C}}{3} = 2\left( {\frac{1}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right) = \frac{1}{R}\left( {1 + b + c} \right) \cr
& \therefore \,\,R = 1\,\,\,\,\,\left( {\because \,1 + b + c \ne 0} \right). \cr
& {\text{So}},\frac{1}{{\sin A}} = 2R = 2 \cr
& \Rightarrow \,\,A = \frac{\pi }{6}. \cr} $$
55.
If in a $$\vartriangle ABC,{a^2} + {b^2} + {c^2} = 8{R^2},$$ where $$R =$$ circumradius, then the triangle is A
equilateral
B
isosceles
C
right angled
D
None of these
Answer :
right angled
View Solution
Discuss Question
$$\eqalign{
& {a^2} + {b^2} + {c^2} = 8{R^2} \cr
& \Rightarrow \,\,{\sin ^2}A + {\sin ^2}B + {\sin ^2}C = 2 \cr
& \Rightarrow \cos 2A + \cos 2B + \cos 2C + 1 = 0 \cr
& \therefore - 4\cos A \cdot \cos B \cdot \cos C = 0 \cr
& \Rightarrow \,\,A\,\,{\text{or }}B\,\,{\text{or }}C = \frac{\pi }{2}. \cr} $$
56.
If in an obtuse-angled triangle the obtuse angle is $$\frac{{3\pi }}{4}$$ and the other two angles are equal to two values of $$\theta $$ satisfying $$a\tan \theta + b\sec \theta = c,$$ where $$\left| b \right| \leqslant \sqrt {{a^2} + {c^2}} ,\,$$ then $${{a^2} - {c^2}}$$ is equal to A
$$ac$$
B
$$2ac$$
C
$$\frac{a}{c}$$
D
None of these
Answer :
$$2ac$$
View Solution
Discuss Question
$$c\cos \theta - a\sin \theta = b.$$ Therefore, $$c\cos\alpha - a\sin \alpha = c\cos \beta - a\sin \beta ,$$ where $$\alpha ,\beta $$ are the other two angles of the triangle.
57.
If $$A + B + C = \pi ,$$ then $$\cos 2A + \cos 2B + \cos 2C + 4\sin A\sin B\sin C$$ is equal to : A
0
B
1
C
2
D
3
Answer :
1
View Solution
Discuss Question
$$\eqalign{
& {\text{If}}\,A + B + C = \pi , \cr
& {\text{then}}\,\,\cos \,mA + \cos \,mB + \cos \,mC \cr
& = 1 - 4\sin \frac{{mA}}{2}\sin \frac{{mB}}{2}\sin \frac{{mC}}{2} \cr
& \therefore {\text{For }}\,m = 2:\cos 2A + \cos 2B + \cos 2C \cr
& = 1 - 4\sin A\sin B\sin C \cr
& \Rightarrow \cos 2A + \cos 2B + \cos 2C + 4\sin A\sin B\sin C = 1 \cr} $$
58.
A tower standing at right angles to the ground subtends an $${\sin ^{ - 1}}\frac{1}{3}$$ and $${\sin ^{ - 1}}\frac{1}{{\sqrt 5 }}$$ at two points $$A$$ and $$B$$ situated in a line through the foot of the tower and on the opposite sides. If $$AB = 50$$ units, then the height of the tower is : A
$$50$$
B
$$25\sqrt 2 $$
C
$$50\left( {\sqrt 6 - 2} \right)$$
D
$$25\left( {\sqrt 2 - 1} \right)$$
Answer :
$$25\left( {\sqrt 2 - 1} \right)$$
View Solution
Discuss Question
$$\eqalign{
& {\sin ^{ - 1}}\frac{1}{3} = {\cot ^{ - 1}}2\sqrt 2 \cr
& {\text{and }}\,{\sin ^{ - 1}}\frac{1}{{\sqrt 5 }} = {\cot ^{ - 1}}2 \cr} $$
If $$C$$ is the foot of the tower and $$h$$ is the height, then
$$AC = h \cdot 2\sqrt 2 ,CB = h \cdot 2,h\left( {2\sqrt 2 + 2} \right) = 50$$
$$ \Rightarrow h = 25\left( {\sqrt 2 - 1} \right)$$
59.
A $$\vartriangle ABC$$ is right angled at $$B.$$ Then the diameter of the incircle of the triangle is A
$$2\left( {c + a - b} \right)$$
B
$$c + a - 2b$$
C
$$c + a - b$$
D
None of these
Answer :
$$c + a - b$$
View Solution
Discuss Question
$$\eqalign{
& r = \frac{\vartriangle }{s} = \frac{{\left( {\frac{1}{2}} \right) \cdot ac}}{{\left( {\frac{1}{2}} \right) \cdot \left( {a + b + c} \right)}} = \frac{{ac}}{{a + b + c}} = \frac{{ac\left( {c + a - b} \right)}}{{{{\left( {c + a} \right)}^2} - {b^2}}} = \frac{{ac\left( {c + a - b} \right)}}{{{c^2} + 2ca + {a^2} - {b^2}}} \cr
& r = \frac{{ac\left( {c + a - b} \right)}}{{2ca + {b^2} - {b^2}}} = \frac{{c + a - b}}{2}\,\,\,\left( {\because \,\,{a^2} + {c^2} = {b^2}} \right). \cr} $$
60.
If the area of a $$\vartriangle ABC$$ be $$\lambda $$ then $${a^2}\sin 2B + {b^2}\sin 2A$$ is equal to A
$$2\lambda $$
B
$$\lambda $$
C
$$4\lambda $$
D
None of these
Answer :
$$4\lambda $$
View Solution
Discuss Question
$$\eqalign{
& {a^2}\sin 2B + {b^2}\sin 2A = 2{a^2}\sin B \cdot \cos B + 2{b^2}\sin A\cos A \cr
& {a^2}\sin 2B + {b^2}\sin 2A = \frac{{{a^2}b}}{R}\cos B + \frac{{{b^2}a}}{R}\cos A \cr
& {a^2}\sin 2B + {b^2}\sin 2A = \frac{{ab}}{R}\left( {a\cos B + b\cos A} \right) = \frac{{abc}}{R} = 2bc\sin A \cr
& {a^2}\sin 2B + {b^2}\sin 2A = 4\left( {\frac{1}{2}bc\sin A} \right) = 4\lambda . \cr} $$