11.
In a $$\vartriangle ABC$$ the sides $$a, b$$ and $$c$$ are in A.P. Then $$\left( {\tan \frac{A}{2} + \tan \frac{C}{2}} \right):\cot \frac{B}{2}$$ is equal to A
3 : 2
B
1 : 2
C
3 : 4
D
None of these
Answer :
None of these
View Solution
Discuss Question
$$\eqalign{
& 2b = a + c \cr
& \Rightarrow \,\,2\sin B = \sin A + \sin C \cr
& \Rightarrow \,\,2\sin \frac{B}{2} = \cos \frac{{A - C}}{2} \cr
& \Rightarrow 2\cos \frac{{A + C}}{2} = \cos \frac{{A - C}}{2} \cr
& \Rightarrow \,\,\cos \frac{A}{2} \cdot \cos \frac{C}{2} = 3\sin \frac{A}{2} \cdot \sin \frac{C}{2} \cr
& \Rightarrow \,\,\tan \frac{A}{2} \cdot \tan \frac{C}{2} = \frac{1}{3} \cr
& \therefore \,\,\frac{{\tan \frac{A}{2} + \tan \frac{C}{2}}}{{\cot \frac{B}{2}}} = \frac{{\cos \frac{B}{2}}}{{\cos \frac{A}{2} \cdot \cos \frac{C}{2}}} \cdot \frac{{\sin \frac{B}{2}}}{{\cos \frac{B}{2}}} = \frac{{\cos \frac{{A + C}}{2}}}{{\cos \frac{A}{2} \cdot \cos \frac{C}{2}}} \cr
& = 1 - \tan \frac{A}{2} \cdot \tan \frac{C}{2} = 1 - \frac{1}{3} = \frac{2}{3}. \cr} $$
12.
In a triangle $$ABC,DC = {90^ \circ }$$ then $$\frac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}}$$ is equal to : A
$$\sin \left( {A + B} \right)$$
B
$$\sin \left( {A - B} \right)$$
C
$$\cos \left( {A + B} \right)$$
D
$$\sin \left( {\frac{{A - B}}{2}} \right)$$
Answer :
$$\sin \left( {A - B} \right)$$
View Solution
Discuss Question
$$\eqalign{
& A + B = {180^ \circ } - C = {90^ \circ } \cr
& a = 2R\sin A,b = 2R\sin B,c = 2R\sin C \cr
& \therefore \frac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}} = \frac{{{{\sin }^2}A - {{\sin }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} \cr
& = \frac{{\sin \left( {A + B} \right)\sin \left( {A - B} \right)}}{{{{\sin }^2}A + {{\sin }^2}\left( {{{90}^ \circ } - A} \right)}}\,\,\,\left[ {\because A + B = {{90}^ \circ }} \right] \cr
& = \frac{{\sin {{90}^ \circ }\sin \left( {A - B} \right)}}{{{{\sin }^2}A + {{\cos }^2}A}} = \sin \left( {A - B} \right) \cr} $$
13.
Two poles are $$10\,m$$ and $$20\,m$$ high. The line joining their tops makes an angle of $${15^ \circ }$$ with the horizontal. The distance between the poles is approximately equal to A
$$36.3\,m$$
B
$$37.3\,in$$
C
$$38.3\,m$$
D
$$39.3\,in$$
Answer :
$$37.3\,in$$
View Solution
Discuss Question
$$\eqalign{
& \tan {15^ \circ } = \frac{{DE}}{{AE}} \cr
& AE = 10\cot {15^ \circ }\,\,\,.....\left( 1 \right) \cr
& \cot \left( {{{15}^ \circ }} \right) = \cot \left( {{{45}^ \circ } - {{30}^ \circ }} \right) \cr
& = \frac{{\cot {{45}^ \circ }\cot {{30}^ \circ } + 1}}{{\cot {{30}^ \circ } - \cot {{45}^ \circ }}} \cr} $$
$$\eqalign{
& \cot {15^ \circ } = \frac{{1 \cdot \sqrt 3 + 1}}{{\sqrt 3 - 1}} = 2 + \sqrt 3 \cr
& {\text{Putting }}\cot {15^ \circ }{\text{ in eq}}\left( 1 \right) \cr
& AE = 10\cot {15^ \circ } \cr
& = 10\left( {2 + \sqrt 3 } \right) \cr
& = 10\left( {3.73} \right) \cr
& = 37.3\,m \cr} $$
14.
Let $$PQR$$ be a triangle of area $$\Delta $$ with $$a = 2,$$ $$b = \frac{7}{2}\,{\text{and }}c = \frac{5}{2};$$ where $$a, b,$$ and $$c$$ are the lengths of the sides of the triangle opposite to the angles at $$PQ$$ and $$R$$ respectively. Then $$\frac{{2\sin P - \sin 2P}}{{2\sin P + \sin 2P}}$$ equals. A
$$\frac{3}{{4\Delta }}$$
B
$$\frac{45}{{4\Delta }}$$
C
$${\left( {\frac{3}{{4\Delta }}} \right)^2}$$
D
$${\left( {\frac{45}{{4\Delta }}} \right)^2}$$
Answer :
$${\left( {\frac{3}{{4\Delta }}} \right)^2}$$
View Solution
Discuss Question
We have,
15.
A man from the top of a 100 metres high tower sees a car moving towards the tower at an angle of depression of 30°. After some time, the angle of depression becomes 60°. The distance (in metres) travelled by the car during this time is A
$$100\sqrt 3 $$
B
$$200\frac{{\sqrt 3 }}{3}$$
C
$$100\frac{{\sqrt 3 }}{3}$$
D
$$200\sqrt 3 $$
Answer :
$$200\frac{{\sqrt 3 }}{3}$$
View Solution
Discuss Question
$$\eqalign{
& {\text{In }}\Delta CBD,\tan {60^ \circ } = \frac{{100}}{3} \cr
& \Rightarrow \,\,x = \frac{{100}}{{\sqrt 3 }} \cr
& {\text{In }}\Delta ACB,\tan {30^ \circ } = \frac{{100}}{{x + d}} \cr
& \Rightarrow \,\,x + d = 100\sqrt 3 \cr
& \Rightarrow \,\,d = 100\sqrt 3 - \frac{{100}}{{\sqrt 3 }} \cr
& = \frac{{200}}{{\sqrt 3 }} \cr
& = \frac{{200\sqrt 3 }}{3}m \cr} $$
16.
In a $$\vartriangle ABC,$$ if $$\tan\frac{A}{2} = \frac{5}{6}$$ and $$\tan\frac{B}{2} = \frac{20}{37}$$ then A
$$2a = b + c$$
B
$$a > b > c$$
C
$$2c = a + b$$
D
None of these
Answer :
$$a > b > c$$
View Solution
Discuss Question
Clearly, $$\tan\frac{A}{2} > \tan \frac{B}{2};$$
17.
In a triangle $$ABC,$$ $$2ac\sin \frac{1}{2}\left( {A - B + C} \right) = $$ A
$${a^2} + {b^2} - {c^2}$$
B
$${c^2} + {a^2} - {b^2}$$
C
$${b^2} - {c^2} - {a^2}$$
D
$${c^2} - {a^2} - {b^2}$$
Answer :
$${c^2} + {a^2} - {b^2}$$
View Solution
Discuss Question
We know that $$A + B + C = 180°$$
18.
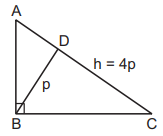
In a $$\vartriangle ABC,B = {90^ \circ },AC = h$$ and the length of the perpendicular from $$B$$ to $$AC$$ is $$p$$ such that $$h = 4p.$$ If $$AB < BC$$ then $$\angle C$$ has the measure A
$$\frac{5\pi }{{12}}$$
B
$$\frac{\pi }{{6}}$$
C
$$\frac{\pi }{{12}}$$
D
None of these
Answer :
$$\frac{\pi }{{12}}$$
View Solution
Discuss Question
Here, $$CD = p\cot C\,\,{\text{and }}AD = p\cot A = p\tan C$$
Adding, $$4p = p\cot C + p\tan C$$
$$\eqalign{
& \Rightarrow \,\,\tan C + \cot C = 4 \cr
& {\text{or, }}\frac{1}{{\sin C \cdot \cos C}} = 4\,\,{\text{or, }}\sin 2C = \frac{1}{2} \cr
& \Rightarrow \,\,C = {15^ \circ }. \cr} $$
19.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is A
60 $$m$$
B
30 $$m$$
C
40 $$m$$
D
20 $$m$$
Answer :
20 $$m$$
View Solution
Discuss Question
From the figure
$$\eqalign{
& \tan {60^ \circ } = \frac{y}{x} \cr
& \Rightarrow \,\,y = \sqrt 3 x\,\,\,\,\,\,\,\,.....\left( 1 \right) \cr
& \tan {30^ \circ } = \frac{y}{{x + 40}} \cr
& \Rightarrow \,\,y = \frac{{x + 40}}{{\sqrt 3 }}\,\,\,\,\,.....\left( 2 \right) \cr} $$
From (1) and (2), $$\sqrt 3 x = \frac{{x + 40}}{{\sqrt 3 }}$$
$$ \Rightarrow \,\,x = 20m$$
20.
If $$R$$ denotes circumradius then in a $$\vartriangle ABC,\frac{{{b^2} - {c^2}}}{{2aR}}$$ is equal to A
$$\cos \left( {B - C} \right)$$
B
$$\sin \left( {B - C} \right)$$
C
$$\cos B - \cos C$$
D
None of these
Answer :
$$\sin \left( {B - C} \right)$$
View Solution
Discuss Question
$$\frac{{{b^2} - {c^2}}}{{2aR}} = \frac{{4{R^2}\left( {{{\sin }^2}B - {{\sin }^2}C} \right)}}{{4{R^2}\sin A}} = \frac{{\sin \left( {B + C} \right)\sin \left( {B - C} \right)}}{{\sin A}} = \sin \left( {B - C} \right).$$