141.
Let $$L\sin \theta = 10 + \log \sin \theta .$$ The number of triangles $$ABC$$ such that $$\log b + 10 = \log c + L\sin B$$ is A
one
B
two
C
infinite
D
None of these
Answer :
one
View Solution
Discuss Question
$$\eqalign{
& \log b + 10 = \log c + 10 + \log \sin B \cr
& \Rightarrow \,\,b = c\sin B \cr
& \Rightarrow \,\,b = b\sin C \cr
& \Rightarrow \,\,\sin C = 1. \cr} $$
142.
In a $$\Delta \,ABC,$$ if $$\frac{{\cos A}}{a} = \frac{{\cos B}}{b} = \frac{{\cos C}}{c},$$ and the side $$a = 2,$$ then are $$a$$ of the triangle is A
$$1$$
B
$$2$$
C
$$\frac{{\sqrt 3 }}{2}$$
D
$$\sqrt 3 $$
Answer :
$$\sqrt 3 $$
View Solution
Discuss Question
$$\eqalign{
& \frac{{\cos A}}{a} = \frac{{\cos B}}{b} = \frac{{\cos C}}{c} \cr
& \Rightarrow \frac{{\cos A}}{{2R\sin A}} = \frac{{\cos B}}{{2R\sin B}} = \frac{{\cos C}}{{2R\sin C}} \cr
& \Rightarrow \cot A = \cot B = \cot C \cr
& \Rightarrow A = B = C = {60^ \circ } \cr
& \Rightarrow \Delta \,ABC{\text{ is equilateral}} \cr
& {\text{Hence}},\,\,\Delta = \frac{{\sqrt 3 }}{4}{a^2} = \sqrt 3 . \cr} $$
143.
In a $$\vartriangle ABC,A = {90^ \circ }.$$ Then $${\tan^{ - 1}}\frac{b}{{a + c}} + {\tan ^{ - 1}}\frac{c}{{a + b}}$$ is equal to A
$$\frac{\pi }{4}$$
B
$$\frac{\pi }{2}$$
C
$${\tan ^{ - 1}}\frac{a}{{b + c}}$$
D
None of these
Answer :
$$\frac{\pi }{4}$$
View Solution
Discuss Question
$$\eqalign{
& {\tan ^{ - 1}}\left( {\frac{a}{{b + c}}} \right) + {\tan ^{ - 1}}\left( {\frac{b}{{c + a}}} \right) \cr
& {\text{We know that }}{\tan ^{ - 1}}x + {\tan ^{ - 1}}y = {\tan ^{ - 1}}\left( {\frac{{x + y}}{{1 - xy}}} \right) \cr
& {\text{Replace, }}x{\text{ by }}\frac{a}{{b + c}}{\text{ and }}y{\text{ by }}\frac{b}{{c + a}} \cr
& = {\tan ^{ - 1}}\left( {\frac{{\frac{a}{{b + c}} + \frac{b}{{c + a}}}}{{1 - \frac{{ab}}{{\left( {b + c} \right)\left( {c + a} \right)}}}}} \right) \cr
& = {\tan ^{ - 1}}\left( {\frac{{\frac{{ac + {a^2} + {b^2} + bc}}{{\left( {b + c} \right)\left( {c + a} \right)}}}}{{\frac{{\left( {b + c} \right)\left( {c + a} \right) - ab}}{{\left( {b + c} \right)\left( {c + a} \right)}}}}} \right) \cr
& = {\tan ^{ - 1}}\left( {\frac{{\frac{{{a^2} + {b^2} + bc + ac}}{{\left( {b + c} \right)\left( {c + a} \right)}}}}{{\frac{{bc + {c^2} + ca}}{{\left( {b + c} \right)\left( {c + a} \right)}}}}} \right) \cr
& = {\tan ^{ - 1}}\frac{{{a^2} + {b^2} + bc + ac}}{{bc + {c^2} + ca}} \cr
& {\text{Given, }}\angle {\text{C = }}{90^ \circ } \Rightarrow {a^2} + {b^2} = {c^2} \cr
& = {\tan ^{ - 1}}\frac{{{c^2} + bc + ac}}{{bc + {c^2} + ca}} \cr
& = {\tan ^{ - 1}}1 \cr
& = \frac{\pi }{4} \cr} $$
144.
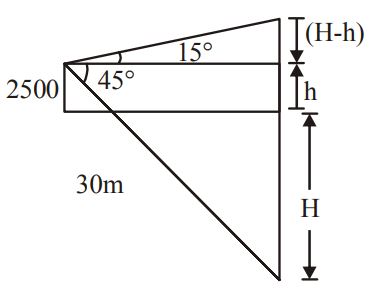
The angle of elevation of a stationary cloud from a point $$2500\,m$$ above a lake is $${15^ \circ }$$ and the angle of depression of its reflection in the lake is $${45^ \circ }.$$ The height of cloud above the lake level is A
$$2500\sqrt 3 \,{\text{metres}}$$
B
$$2500 \,{\text{metres}}$$
C
$$500\sqrt 3 \,{\text{metres}}$$
D
None of these
Answer :
$$2500\sqrt 3 \,{\text{metres}}$$
View Solution
Discuss Question
$$\eqalign{
& \left( {H - h} \right)\cot {15^ \circ } = \left( {H + h} \right)\cot {45^ \circ } \cr
& {\text{or }}H = \frac{{h\left( {\cot {{15}^ \circ } + 1} \right)}}{{\left( {\cot {{15}^ \circ } - 1} \right)}} \cr} $$
Since $$h = 2500$$ and substitute
$$\cot {15^ \circ } = 2 + \sqrt 3 ,{\text{ we get, }}H = 2500\sqrt 3 $$