121. In a $$\vartriangle ABC,$$ the sides $$a, b$$ and $$c$$ are such that they are the roots of $${x^3} - 11{x^2} + 38x - 40 = 0.$$ Then $$\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}$$ is equal to
A
$$\frac{3}{4}$$
B
$$1$$
C
$$\frac{9}{16}$$
D
None of these
Answer :
$$\frac{9}{16}$$
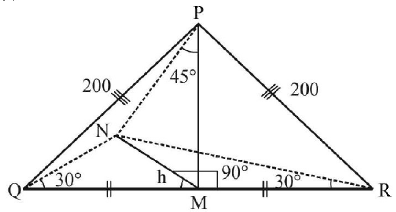
122. $$PQR$$ is a triangular park with $$PQ = PR = 200 m.$$ A. T. V. tower stands at the mid - point of $$QR.$$ If the angles of elevation of the top of the tower at $$P, Q$$ and $$R$$ are respectively 45°, 30° and 30°, then the height of the tower (in $$m$$ ) is:
A
50
B
$$100\sqrt 3 $$
C
$$50\sqrt 2 $$
D
100
Answer :
100
123. In a $$\vartriangle ABC,$$ the sides are in the ratio 4 : 5 : 6. The ratio of the circumradius and the inradius is
A
8 : 7
B
3 : 2
C
7 : 3
D
16 : 7
Answer :
16 : 7
124. In a triangle $$ABC,$$ angle $$A$$ is greater than angle $$B.$$ If the measures of angles $$A$$ and $$B$$ satisfy the equation $$3\sin x - 4{\sin ^3}x - k = 0, 0 < k < 1,$$ then the measure of angle $$C$$ is
A
$$\frac{\pi }{3}$$
B
$$\frac{\pi }{2}$$
C
$$\frac{2\pi }{3}$$
D
$$\frac{5\pi }{6}$$
Answer :
$$\frac{2\pi }{3}$$
125. Angles of a triangle are in the ratio $$4 : 1 : 1.$$ The ratio between its greatest side and perimeter is
A
$$\frac{3}{{2 + \sqrt 3 }}$$
B
$$\frac{1}{{2 + \sqrt 3 }}$$
C
$$\frac{\sqrt 3}{{\sqrt 3 + 2 }}$$
D
$$\frac{2}{{2 + \sqrt 3 }}$$
Answer :
$$\frac{\sqrt 3}{{\sqrt 3 + 2 }}$$
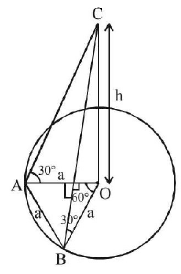
126. A tower stands at the centre of a circular park. $$A$$ and $$B$$ are two points on the boundary of the park such that $$AB (= a)$$ subtends an angle of 60° at the foot of the tower, and the angle of elevation of the top of the tower from $$A$$ or $$B$$ is 30°. The height of the tower is
A
$$\frac{a}{{\sqrt 3 }}$$
B
$$a\sqrt 3 $$
C
$$\frac{2a}{{\sqrt 3 }}$$
D
$$2a\sqrt 3 $$
Answer :
$$\frac{a}{{\sqrt 3 }}$$
127. If in a $$\vartriangle ABC,{a^2}{\cos ^2}A = {b^2} + {c^2}$$ then
A
$$A < \frac{\pi }{4}$$
B
$$\frac{\pi }{4} < A < \frac{\pi }{2}$$
C
$$A > \frac{\pi }{2}$$
D
$$A = \frac{\pi }{2}$$
Answer :
$$A > \frac{\pi }{2}$$
128. In a $$\vartriangle ABC,$$ the inradius and three exradii are $$r,{r_1},{r_2}$$ and $${r_3}$$ respectively. In usual notations the value of $$r \cdot {r_1} \cdot {r_2} \cdot {r_3}$$ is equal to
A
$$2\vartriangle $$
B
$${\vartriangle ^2}$$
C
$$\frac{{abc}}{{4R}}$$
D
None of these
Answer :
$${\vartriangle ^2}$$
129. In a triangle $$ABC,$$ $$\angle B = \frac{\pi }{3}{\text{ and }}\angle C = \frac{\pi }{4}.$$ Let $$D$$ divide $$BC$$ internally in the ratio 1 : 3 then $$\frac{{\sin \angle BAD}}{{\sin \angle CAD}}$$ is equal to
A
$$\frac{1}{{\sqrt 6 }}$$
B
$${\frac{1}{3}}$$
C
$$\frac{1}{{\sqrt 3 }}$$
D
$$\sqrt {\frac{2}{3}} $$
Answer :
$$\frac{1}{{\sqrt 6 }}$$
130. In a $$\vartriangle ABC,B = \frac{\pi }{8}$$ and $$C = \frac{{5\pi }}{8}.$$ The altitude from $$A$$ to the side $$BC$$ is
A
$$\frac{a}{2}$$
B
$$2a$$
C
$$\frac{1}{2}\left( {b + c} \right)$$
D
None of these
Answer :
$$\frac{a}{2}$$